题目内容
用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质,以及怎样变形的:
(1)如果2x+7=10.那么2x=10-
(2)如果
=2,那么a=
(3)如果2a=1.5.那么6a=
(4)如果-5x=5y;那么x=
(1)如果2x+7=10.那么2x=10-
-7(等式的两边同时减去7,等式仍成立)
-7(等式的两边同时减去7,等式仍成立)
;(2)如果
| a | 4 |
8(等式的两边同时乘以4,等式仍成立)
8(等式的两边同时乘以4,等式仍成立)
;(3)如果2a=1.5.那么6a=
4.5(等式的两边同时乘以3,等式仍成立)
4.5(等式的两边同时乘以3,等式仍成立)
;(4)如果-5x=5y;那么x=
-y(等式的两边同时除以-5,等式仍成立)
-y(等式的两边同时除以-5,等式仍成立)
.分析:根据等式的基本性质进行填空.
解答:解:(1)根据等式的性质1,若2x+7=10,则2x=10-7(等式的两边同时减去7,等式仍成立);
故填:-7(等式的两边同时减去7,等式仍成立);
(2)根据等式性质2,若
=2,则a=8(等式的两边同时乘以4,等式仍成立);
故填:8(等式的两边同时乘以4,等式仍成立);
(3)根据等式性质2,若2a=1.5,则6a=4.5(等式的两边同时乘以3,等式仍成立);
故填:4.5(等式的两边同时乘以3,等式仍成立);
(4)根据等式性质2,若-5x=5y,则x=-y(等式的两边同时除以-5,等式仍成立);
故填:-y(等式的两边同时除以-5,等式仍成立).
故填:-7(等式的两边同时减去7,等式仍成立);
(2)根据等式性质2,若
| a |
| 4 |
故填:8(等式的两边同时乘以4,等式仍成立);
(3)根据等式性质2,若2a=1.5,则6a=4.5(等式的两边同时乘以3,等式仍成立);
故填:4.5(等式的两边同时乘以3,等式仍成立);
(4)根据等式性质2,若-5x=5y,则x=-y(等式的两边同时除以-5,等式仍成立);
故填:-y(等式的两边同时除以-5,等式仍成立).
点评:本题主要考查了等式的基本性质.
等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.
等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
相关题目
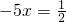 ,则x=______;
,则x=______;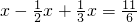 ,则______=
,则______= .
. x-11=5,那么
x-11=5,那么 x=5+________;
x=5+________; t=
t= ,那么t=_________。
,那么t=_________。