题目内容
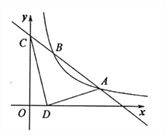
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图像恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图像恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) 
A.3
B.4
C.6
D.8
【答案】C
【解析】解:设点C坐标为(x,y),作CD⊥BO′交边BO′于点D, 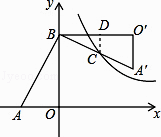
∵tan∠BAO=2,
∴ ![]() =2,
=2,
∵S△ABO= ![]() AOBO=4,
AOBO=4,
∴AO=2,BO=4,
∵△ABO≌△A'O'B,
∴AO=A′O′=2,BO=BO′=4,
∵点C为斜边A′B的中点,CD⊥BO′,
∴CD= ![]() A′O′=1,BD=
A′O′=1,BD= ![]() BO′=2,
BO′=2,
∴x=BO﹣CD=4﹣1=3,y=BD=2,
∴k=xy=32=6.
故选C.
【考点精析】掌握比例系数k的几何意义是解答本题的根本,需要知道几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
相关题目