题目内容
如图所示,⊙O的内接△ABC的AB边过圆心O,CD切⊙O于C,BD⊥CD于D,交⊙O于F,CE⊥AB于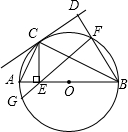 点E,FE交⊙O于G.
点E,FE交⊙O于G.解答下列问题:
(1)若BC=10,BE=8,求CD的值;
(2)求证:DF•DB=EG•EF.
分析:(1)根据切线的性质及圆周角定理等可得到CE=CD,因此只要求出CE就可求出CD,CE可通过勾股定理来求解.
(2)根据切割线定理及相似三角形的判定即可得到所求的结论.
(2)根据切割线定理及相似三角形的判定即可得到所求的结论.
解答:(1)解:∵AB为直径,BD⊥CD
∴∠ABC+∠A=90°,∠CBD+∠BCD=90°
∵CD为⊙O切线
∴∠BCD=∠A
∴∠ABC=∠BCD
∵CD⊥BD,CE⊥BE
∴CE=CD
∴CE=
=
=6
∴CD=6
(2)证明:∵CD为切线,BD为割线
∴CD2=DF•DB①
∵∠ACB=90°,CE⊥AB
∴RT△ACE∽RT△CBE
∴CE2=EA•EB②
∵EG•EF=EA•EB③
由①②③及CD=CE得DF•DB=EG•EF.
∴∠ABC+∠A=90°,∠CBD+∠BCD=90°
∵CD为⊙O切线
∴∠BCD=∠A
∴∠ABC=∠BCD
∵CD⊥BD,CE⊥BE
∴CE=CD
∴CE=
| BC2-BE2 |
| 100-64 |
∴CD=6
(2)证明:∵CD为切线,BD为割线
∴CD2=DF•DB①
∵∠ACB=90°,CE⊥AB
∴RT△ACE∽RT△CBE
∴CE2=EA•EB②
∵EG•EF=EA•EB③
由①②③及CD=CE得DF•DB=EG•EF.
点评:此题主要考查相似的判定,切割线定理,相交弦定理以及勾股定理的综合运用.

练习册系列答案
相关题目
 23、如图所示,⊙O的内接△ABC中,AB=AC,D是BC边上的一点直线AD交⊙O于E.
23、如图所示,⊙O的内接△ABC中,AB=AC,D是BC边上的一点直线AD交⊙O于E.
 如图所示,⊙O的内接三角形ABC中,AC=BC,CD平分∠ACB,交圆O于点D,下列结论:
如图所示,⊙O的内接三角形ABC中,AC=BC,CD平分∠ACB,交圆O于点D,下列结论:
 为
为 的内接三角形,
的内接三角形, 则
则