题目内容
 23、如图所示,⊙O的内接△ABC中,AB=AC,D是BC边上的一点直线AD交⊙O于E.
23、如图所示,⊙O的内接△ABC中,AB=AC,D是BC边上的一点直线AD交⊙O于E.(1)求证:AB2=AD•AE;
(2)当点D在BC的延长线上时,(1)的结论还成立吗?若成立,给出证明;若不成立,请说明理由.
分析:(1)连接BE,可得△ABE∽△ADB,根据相似三角形的性质得出结论.
(2)成立,可证△AEB∽△ABD,可得AB2=AD•AE.
(2)成立,可证△AEB∽△ABD,可得AB2=AD•AE.
解答:证明:(1)连接BE,∵AB=AC,
∴∠ABC=∠C.
∵∠E=∠C,
∴∠ABC=∠E.
∵∠BAE=∠DAB,
∴△ABE∽△ADB.
∴AB:AD=AE:AB.(2分)
∴AB2=AD•AE.(4分)
(2)成立.(5分)
∵AB=AC,
∴∠ABC=∠ACB.
∵∠EBD=∠DBE,∠ABE=∠ABC-∠EBD,∠D=∠ACB-∠CAD,
∵∠BAD为公共角,
∴△AEB∽△ABD.(7分)
∴AB:AD=AE:AB.
∴AB2=AD•AE.(8分)
∴∠ABC=∠C.
∵∠E=∠C,
∴∠ABC=∠E.
∵∠BAE=∠DAB,
∴△ABE∽△ADB.
∴AB:AD=AE:AB.(2分)
∴AB2=AD•AE.(4分)
(2)成立.(5分)
∵AB=AC,
∴∠ABC=∠ACB.
∵∠EBD=∠DBE,∠ABE=∠ABC-∠EBD,∠D=∠ACB-∠CAD,
∵∠BAD为公共角,
∴△AEB∽△ABD.(7分)
∴AB:AD=AE:AB.
∴AB2=AD•AE.(8分)
点评:乘积的形式通常可以转化成比例的形式,本题考查了相似三角形的判断和性质.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
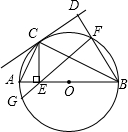 点E,FE交⊙O于G.
点E,FE交⊙O于G.
 如图所示,⊙O的内接三角形ABC中,AC=BC,CD平分∠ACB,交圆O于点D,下列结论:
如图所示,⊙O的内接三角形ABC中,AC=BC,CD平分∠ACB,交圆O于点D,下列结论:
 为
为 的内接三角形,
的内接三角形, 则
则