题目内容
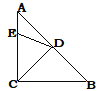
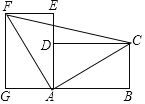
【题目】如图,将两块完全相同的矩形纸片ABCD和矩形纸片AEFG按图示方式放置(点A、D、E在同一直线上),连接AC、AF、CF,已知AD=3,DC=4,则CF的长是( )
A.5B.7C.5![]() D.10
D.10
【答案】C
【解析】
由两块完全相同的矩形纸片ABCD和矩形纸片AEFG,得出AG=AD=BC=3,FG=AB=CD=4,∠FGA=∠ABC=90°,由勾股定理求出AC=5,由SAS证得△FGA≌△ABC,得出AF=AC,∠GFA=∠BAC,∠GAF=∠BCA,由∠GFA+∠GAF=90°,推出∠GAF+BAC=90°,得出∠FAC=90°,即△CAF是等腰直角三角形,即可得出结果.
∵两块完全相同的矩形纸片ABCD和矩形纸片AEFG,
∴AG=AD=BC=3,FG=AB=CD=4,∠FGA=∠ABC=90°,
AC=![]() =5,
=5,
在△FGA和△ABC中,
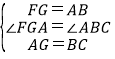 ,
,
∴△FGA≌△ABC(SAS),
∴AF=AC,∠GFA=∠BAC,∠GAF=∠BCA,
∵∠GFA+∠GAF=90°,
∴∠GAF+BAC=90°,
∴∠FAC=90°,
∴△CAF是等腰直角三角形,
∴CF=![]() AC=5
AC=5![]() ,
,
故选C.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目