题目内容
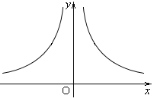
【题目】平面直角坐标系中,点A在函数y1=![]() (x>0)的图象上,点B在y2=-
(x>0)的图象上,点B在y2=-![]() (x<0)的图象上,设A的横坐标为a,B的横坐标为b:
(x<0)的图象上,设A的横坐标为a,B的横坐标为b:
(1)当|a|=|b|=5时,求△OAB的面积;
(2)当AB∥x轴时,求△OAB的面积;
(3)当△OAB是以AB为底边的等腰三角形,且AB与x轴不平行时,求a![]() b的值.
b的值.
【答案】(1)、2;(2)、2;(3)、-2.
【解析】
试题分析:(1)、根据题意分析得出点A和B的坐标,然后计算面积;(2)、分别设出点A和B的坐标,根据平行得出a和b的关系,然后进行计算面积;(3)、根据题意得出点A、B的坐标,根据等腰直角三角形的性质和勾股定理得出等式,然后求出a![]() b的值.
b的值.
试题解析:(1)、∵a>0,b<0,当|a|=|b|=5时,可得A(5,![]() ),B(-5,
),B(-5,![]() )
)
∴S△OAB=![]() ×10×
×10×![]() =2
=2
(2)、设A(a,![]() ),B(b,
),B(b,![]() ),当AB∥x轴时,
),当AB∥x轴时,![]() =
=![]() ,∴a=-b
,∴a=-b
∴S△OAB=![]() ×(a-b)×
×(a-b)×![]() =
=![]() ×2 a×
×2 a×![]() =2
=2
(3)、设A(a,![]() ),B(b,
),B(b,![]() ),∵△OAB是以AB为底边的等腰三角形, OA=OB
),∵△OAB是以AB为底边的等腰三角形, OA=OB
由OA2=a2+(![]() )2 , OB2=a2+(
)2 , OB2=a2+(![]() )2 ,∴a2+(
)2 ,∴a2+(![]() )2=b2+(
)2=b2+(![]() )2
)2
整理得:( a2―b2)(1![]() )=0
)=0
∵AB与x轴不平行,∴|a|≠| b|,∴1![]() =0 ∴a
=0 ∴a![]() b=±2
b=±2
∵a>0,b<0,∴a![]() b=-2
b=-2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目