题目内容
2010年4月14日，在青海玉树发生7.1级地震．在抗震救灾中，某求援队探测出一建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A、B相距3米，探测线与地面夹角分别是30°和60°（如图），则生命所在点C的深度为 （保留根号）．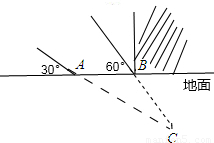
【答案】分析：过C点作AB的垂线交AB的延长线于点D，由三角形外角的性质可得出∠ACB=30°，进而可得出BC=AB=3，在Rt△CDB中利用锐角三角函数的定义即可求出CD的值．
解答：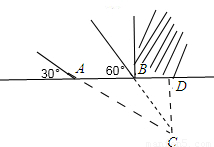
解：过C点作AB的垂线交AB的延长线于点D，
∵∠CAD=30°，∠CBD=60°，
∴∠ACB=30°，
∴∠CAB=∠ACB=30°，
∴BC=AB=3，
在Rt△CDB中，BC=3，∠CBD=60°，sin∠CBD=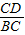
，
∴sin60°=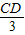
，
∴CD=3sin60°=3×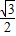
=
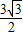（米）．
故答案为：
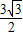米．
点评：本题考查的是解直角三角形的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
解答：
解：过C点作AB的垂线交AB的延长线于点D，∵∠CAD=30°，∠CBD=60°，
∴∠ACB=30°，
∴∠CAB=∠ACB=30°，
∴BC=AB=3，
在Rt△CDB中，BC=3，∠CBD=60°，sin∠CBD=
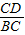，∴sin60°=
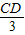，∴CD=3sin60°=3×
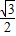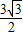=（米）．故答案为：
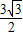米．点评：本题考查的是解直角三角形的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
2010年4月14日7时49分，我国青海玉树发生了7.1级大地震，给玉树人民的生命财产带来巨大损失．地震发生后，我市人民积极响应党中央号召支援灾区，计划募捐药品、食品共100吨运往灾区，若每辆车只能装运同一种物资且必须装满．根据下表提供的信息，解答下列问题．
（1）若装运药品的车辆数为x，装运食品的车辆数为y，求y与x之间的函数关系式；
（2）如果装运每种物资的车辆数至少6辆，那么车辆安排方案有几种？写出每种安排安案；
（3）若要使此次运输费用最小，应采用哪种方案，并求出最少运费．
| 物资名称 | 药品 | 食品 |
| 每辆车运载量（吨） | 5 | 10 |
| 每吨货物运输所用费用（元） | 800 | 600 |
（2）如果装运每种物资的车辆数至少6辆，那么车辆安排方案有几种？写出每种安排安案；
（3）若要使此次运输费用最小，应采用哪种方案，并求出最少运费．
