题目内容
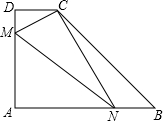 (2013•同安区一模)如图所示,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,tanB=1.动点M、N分别从点D、B同时出发,沿线段DA和BA向A方向运动,动点N的运动速度是动点M运动速度的两倍,当点M或点N谁先运动到点A时,M、N两点同时停止运动.设动点M的运动速度是1个单位/秒,M、N运动的时间为x秒.
(2013•同安区一模)如图所示,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,tanB=1.动点M、N分别从点D、B同时出发,沿线段DA和BA向A方向运动,动点N的运动速度是动点M运动速度的两倍,当点M或点N谁先运动到点A时,M、N两点同时停止运动.设动点M的运动速度是1个单位/秒,M、N运动的时间为x秒.(1)当x=1时,求MN的长;
(2)是否存在x的值,使得△CMN是直角三角形?若存在,求出所有符合条件的x值;若不存在请说明理由.
分析:(1)首先求得AM、AN的长度,然后在直角△AMN中利用勾股定理即可求得;
(2)过C作CE⊥AB,垂足为E,利用运动时间x秒表示出CM、CN、MN的长,然后分∠CMN=90°,∠MCN=90°和∠MNC=90°三种情况进行讨论,依据勾股定理即可列方程求得x的值.
(2)过C作CE⊥AB,垂足为E,利用运动时间x秒表示出CM、CN、MN的长,然后分∠CMN=90°,∠MCN=90°和∠MNC=90°三种情况进行讨论,依据勾股定理即可列方程求得x的值.
解答:解:(1)当x=1时,DM=1,BN=2
∵AB=6,AD=4
∴AM=3,AN=4
∵∠A=90°
∴MN=
=5;
(2)存在.
过C作CE⊥AB,垂足为E,
∵DA⊥AB,
∴DA‖CE,
∵DC‖AE
∴四边形AECD是平行四边形,
∴CE=AD=4,AE=DC=2
在Rt△CEB中
∵tanB=1
∴CE=BE=4
当运动x秒时,DM=x,NB=2x,AN=6-2x,AM=4-x,EN=|4-2x|,(0≤x≤3)
∴CM2=4+x2,MN2=(4-x)2+(6-2x)2=52-32x+5x2,
CN2=16+(4-2x)2=32-16x+4x2,
1)当∠CMN=90°时,CN2=CM2+MN2,
∴32-16x+4x2=4+x2+52-32x+5x2,
解得:x=2或6(舍去),
∴当x=2时,△CMN是直角三角形;
2)当∠MCN=90°时,MN2=CM2+CN2,
则32-16x+4x2+4+x2=52-32x+5x2,
解得:x=1,
∴当x=1时,△CMN是直角三角形;
3)当∠MNC=90°时,CM2=MN2+CN2,
则32-16x2+4x2=4+x2-52+32x-5x2,
即x2-6x+10=0,
方程无解.
∵AB=6,AD=4
∴AM=3,AN=4
∵∠A=90°
∴MN=
| AM2+AN2 |
(2)存在.

过C作CE⊥AB,垂足为E,
∵DA⊥AB,
∴DA‖CE,
∵DC‖AE
∴四边形AECD是平行四边形,
∴CE=AD=4,AE=DC=2
在Rt△CEB中
∵tanB=1
∴CE=BE=4
当运动x秒时,DM=x,NB=2x,AN=6-2x,AM=4-x,EN=|4-2x|,(0≤x≤3)
∴CM2=4+x2,MN2=(4-x)2+(6-2x)2=52-32x+5x2,
CN2=16+(4-2x)2=32-16x+4x2,
1)当∠CMN=90°时,CN2=CM2+MN2,
∴32-16x+4x2=4+x2+52-32x+5x2,
解得:x=2或6(舍去),
∴当x=2时,△CMN是直角三角形;
2)当∠MCN=90°时,MN2=CM2+CN2,
则32-16x+4x2+4+x2=52-32x+5x2,
解得:x=1,
∴当x=1时,△CMN是直角三角形;
3)当∠MNC=90°时,CM2=MN2+CN2,
则32-16x2+4x2=4+x2-52+32x-5x2,
即x2-6x+10=0,
方程无解.
点评:本题考查了勾股定理和直角梯形的综合应用,正确利用x表示出CM、CN、MN的长是关键.

练习册系列答案
相关题目
 (2013•同安区一模)如图几何体的俯视图是( )
(2013•同安区一模)如图几何体的俯视图是( ) (2013•同安区一模)一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示,当0≤x≤1时,y关于x的函数解析式为y=60x;那么当1≤x≤2时,y关于x的函数解析式为( )
(2013•同安区一模)一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示,当0≤x≤1时,y关于x的函数解析式为y=60x;那么当1≤x≤2时,y关于x的函数解析式为( ) (2013•同安区一模)如图,已知:DE∥BC,∠ABC=40°,则∠ADE=
(2013•同安区一模)如图,已知:DE∥BC,∠ABC=40°,则∠ADE=