Question

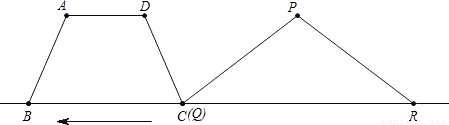
（2008•广州）如图，在梯形ABCD中，AD∥BC，AB=AD=DC=2cm，BC=4cm，在等腰△PQR中，∠QPR=120°，底边QR=6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米．
（1）当t=4时，求S的值；
（2）当4≤t≤10，求S与t的函数关系式，并求出S的最大值．

Answer 1

【答案】分析：（1）首先判定当t=4时，点B与点Q重合，点P与点D重合，则求△BDC的面积即可．
（2）分别从4≤t＜6与6≤t≤10去分析，求得各自的函数解析式，再分析各种情况下的最大值即可求得答案．
解答：解：（1）当t=4时，CQ=4cm，
过点A作AE⊥BC于E，过点D作DF⊥BC于F，
∵AE=DF=cm，∠AEB=∠DFC=90°，AB=CD，
∴△ABE≌△DFC，
∴BE=CF，
∵EF=AD=2cm，BC=4cm，
∴BE=CF=1cm，
∴点D与点P重合，
∴S_△BDC=BC•DF=×4×=2（cm²）；
（2）当4≤t＜6时，P在线段AD上，作KH⊥QH，过点M作MN⊥BC于N，
∵∠Q=30°，∠1=60°，
∴∠2=∠1-∠Q=30°，
∠3=∠2=30°，
∴QB=BM=QC-BC=t-4，
∵∠R=∠Q=30°，∠DCB=∠ABC=60°，
∴∠CKR=∠DCB-∠R=30°=∠R，
∴KC=CR=6-t，
∴HK=KC•sin60°=（6-t）
∴同理：MN=（t-4），
∴S=S_△PQR-S_△BQM-S_△CRK=QR•PG-BQ•EM-CR•FN
=×6×-×（t-4）²-×（6-t）²=-t²+5t-10，
∵a=-＜0，开口向下，
∴S有最大值，
当t=-=5时，S最大值为；
当6≤t≤10时，P在线段DA的延长线上，
∵∠1=60°，∠2=30°，
∴∠3=90°
∴RC=t-6，BR=4-RC=4-（t-6）=10-t，
∴TB=BR=，TR=BR=（10-t），
∴S=TB•TR=××（10-t）=t²-t+，
当a＞0时，开口向上，-=10，
∴t=6时，S最大值为2；
综上，t=5时，S最大值为．
点评：本小题主要考查等腰三角形、等腰梯形、解直角三角形、二次函数等基础知识，考查运算能力、推理能力和空间观念．