题目内容
 (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点.
的图象相交于A、B两点.(1)根据图象,分别写出A、B的坐标;
(2)求出两函数解析式;
(3)根据图象回答:当x为何值时,一次函数的函数值>反比例函数的函数值.
【答案】分析:(1)直接由图象就可得到A(-6,-2)、B(4,3);
(2)把点A、B的坐标代入两函数的解析式,利用方程组求出k、b、m的值,即可得到两函数解析式;
(3)结合图象,分别在第一、二象限求出一次函数的函数值>反比例函数的函数值的x的取值范围.
解答:解:(1)由图象得A(-6,-2),B(4,3).(4分)
(2)设一次函数的解析式为y=kx+b,
把A、B点的坐标代入得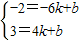
解得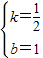 ,
,
所以一次函数的解析式为y= x+1,
x+1,
设反比例函数的解析式为y=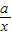 ,把A点坐标代入得
,把A点坐标代入得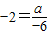 ,解得a=12,
,解得a=12,
所以反比例函数的解析式为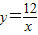 .(4分)
.(4分)
(3)当-6<x<0或x>4时一次函数的值>反比例函数的值.(2分)
点评:本类题目主要考查一次函数、反比例函数的图象和性质,考查待定系数法求函数解析式的基本方法,以及从平面直角坐标系中读图获取有效信息的能力,考查数形结合的数学思想,另外,还需灵活运用方程组解决相关问题.
(2)把点A、B的坐标代入两函数的解析式,利用方程组求出k、b、m的值,即可得到两函数解析式;
(3)结合图象,分别在第一、二象限求出一次函数的函数值>反比例函数的函数值的x的取值范围.
解答:解:(1)由图象得A(-6,-2),B(4,3).(4分)
(2)设一次函数的解析式为y=kx+b,
把A、B点的坐标代入得
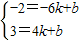
解得
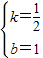 ,
,所以一次函数的解析式为y=
 x+1,
x+1,设反比例函数的解析式为y=
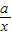 ,把A点坐标代入得
,把A点坐标代入得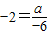 ,解得a=12,
,解得a=12,所以反比例函数的解析式为
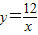 .(4分)
.(4分)(3)当-6<x<0或x>4时一次函数的值>反比例函数的值.(2分)
点评:本类题目主要考查一次函数、反比例函数的图象和性质,考查待定系数法求函数解析式的基本方法,以及从平面直角坐标系中读图获取有效信息的能力,考查数形结合的数学思想,另外,还需灵活运用方程组解决相关问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点.
的图象相交于A、B两点. (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点.
的图象相交于A、B两点. (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点.
的图象相交于A、B两点.