题目内容
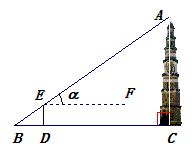
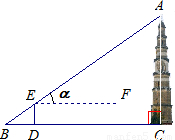
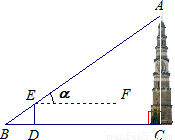
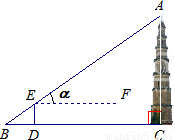
如图,为了对我市城区省级文物保护对象--高AC约42米的天然塔(清乾隆五十七年重修)进行保护性维修,工人要在塔顶A和塔底所在地面上的B处之间拉一根铁丝,在BC上的点D处测得塔顶的仰角α为43°(测倾器DE高1.6米,A,E,B三点在同一条直线上).求∠BAC的度数和铁丝AB的长.(接头部分的长度忽略不计,结果精确到0.1米.sin43°≈0.68,tan43°≈0.93)
【答案】分析:首先分析图形:根据题意构造直角三角形Rt△ABC;先有仰角定义求得∠BAC的度数,再根据三角函数的定义可求得AB=42÷sin43°,解出答案即可.
解答:解:∵BC∥EF,
∴∠AEF=∠B=43°,
∵∠ACB=90°,
∴∠BAC=90°-43°=47°,
在Rt△ABC中,sinB=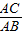 =
= ,
,
∴AB=42÷sin43°≈(5分)42÷0.68≈61.8(米),
答:∠BAC=47°,铁丝的长度是61.8米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
解答:解:∵BC∥EF,
∴∠AEF=∠B=43°,
∵∠ACB=90°,
∴∠BAC=90°-43°=47°,
在Rt△ABC中,sinB=
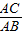 =
= ,
,∴AB=42÷sin43°≈(5分)42÷0.68≈61.8(米),
答:∠BAC=47°,铁丝的长度是61.8米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
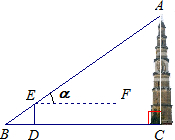 如图,为了对我市城区省级文物保护对象--高AC约42米的天然塔(清乾隆五十七年重修)进行保护性维修,工人要在塔顶A和塔底所在地面上的B处之间拉一根铁丝,在BC上的点D处测得塔顶的仰角α为43°(测倾器DE高1.6米,A,E,B三点在同一条直线上).求∠BAC的度数和铁丝AB的长.(接头部分的长度忽略不计,结果精确到0.1米.sin43°≈0.68,tan43°≈0.93)
如图,为了对我市城区省级文物保护对象--高AC约42米的天然塔(清乾隆五十七年重修)进行保护性维修,工人要在塔顶A和塔底所在地面上的B处之间拉一根铁丝,在BC上的点D处测得塔顶的仰角α为43°(测倾器DE高1.6米,A,E,B三点在同一条直线上).求∠BAC的度数和铁丝AB的长.(接头部分的长度忽略不计,结果精确到0.1米.sin43°≈0.68,tan43°≈0.93)