题目内容
如图，在⊙O中，半径OA⊥弦BC，∠AOB=60°，则圆周角∠ADC=30°
30°
．分析：先由半径OA⊥弦BC，根据垂径定理得到弧AC=弧AB，然后根据圆周角定理求解．
解答：解：∵半径OA⊥弦BC，
∴弧AC=弧AB，
∴∠ADC=
∠AOB=
×60°=30°．
故答案为30°．
∴弧AC=弧AB，
∴∠ADC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为30°．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理．
练习册系列答案
走进文言文系列答案
相关题目
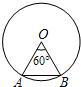19、如图，在⊙O中，半径为5，∠AOB=60°，则弦长AB=
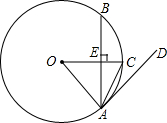（2013•平凉）如图，在⊙O中，半径OC垂直于弦AB，垂足为点E．
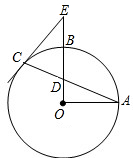如图，在⊙O中，半径OA⊥OB，弦AC交OB于点D，E是OB延长线上一点，如果∠OAD=30°，ED=CE．