Question

【题目】在矩形中，，点,,,开始时分别在点,,,处，同时出发。点,分别按,的方向以1的速度匀速运动，点，分别按,的方向以2的速度匀速运动，当一个点到达端点时，其他各点都停止运动。

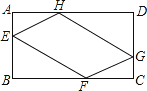
（1）在运动中，点,,,所形成的四边形为哪种四边形，并说明理由。

（2）运动几秒时，四边形的面积为4 ，此时又是何种四边形？

（3）在运动过程中，四边形的面积能否为5，请简要说明理由。

Answer 1

【答案】（1）平行四边形，理由见解析；（2）四边形EFGH是菱形；（3）在运动过程中，四边形EFGH的面积可以为5cm2．

【解析】

试题分析：（1）利用已知得出△AEH≌△CGF，△EBF≌△GDH，再利用平行四边形的判定得出四边形EFGH为平行四边形；

（2）根据四边形EFGH的面积为4cm2，结合运动速度即可得出正好是1秒分别走到各自中点时．

（3）根据运动时四边形EFGH的面积4是最小面积，8是最大面积即可得出答案．

试题解析：（1）平行四边形，

∵E、G，F、D速度分别相同，因此走过距离相同，

AE=CG，EB=DG，BF=DH，AH=CF，

∴△AEH≌△CGF，△EBF≌△GDH，

∴EF=HG，FG=EH，

∴在运动中，点E，F，G，H所形成的四边形EFGH为平行四边形；

（2）∵矩形ABCD中，AB=2cm，BC=4cm，

∴矩形面积为8cm2，

∵四边形EFGH的面积为4cm2，正好是1秒分别走到各自中点时．

运用（1）中证明方法可以得出△AEH≌△CGF≌△EBF≌△GDH，

∴EF=HG=FG=EH，

∴四边形EFGH是菱形；

（3）在运动过程中，四边形EFGH的面积可以为5cm2．

∵4是最小面积，8是最大面积，总有一个时候面积是5．