Question

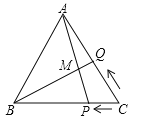
【题目】如图，等边的边长为，点从点出发，以秒的速度由向匀速运动，点从点出发，以秒的速度由向匀速运动，、交于点，当点到达点时，、两点停止运动，设、两点运动的时间为秒，若时，则的值是(　　)

A.B.C.D.

Answer 1

【答案】C

【解析】

由等边三角形性质可得:AC＝BC＝AB＝8cm，∠BAC＝∠ABC＝∠C＝60°，根据题意可得CP＝tcm，CQ＝2rcm，进而可得BP＝(8-t)cm，AQ＝(8-2t)cm，根据三角形外角性质可得∠ABQ＝∠CAP，即可证明△ABQ≌△CAP(ASA)，即可求得的值.

∵△ABC是等边三角形，

∴AC＝BC＝AB＝8cm，∠BAC＝∠ABC＝∠C＝60°，

由题意得，

∴

∵，

∴∠ABQ＝∠CAP，

在△ABQ和△CAP中，

，

∴

∴，

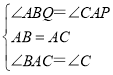∴解得秒.

故答案为C.