题目内容
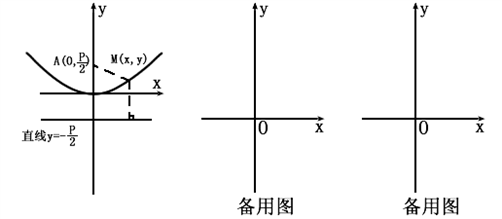
我们知道二次函数的图象是抛物线,它也可以这样定义:如果一个动点M(x,y)到定A(0, 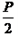 )的距离与它到定直线y= -
)的距离与它到定直线y= -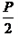 的距离相等,那么动点M形成的图形就是抛物线
的距离相等,那么动点M形成的图形就是抛物线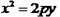 (p>0),如图。
(p>0),如图。
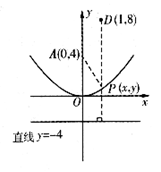
(1)已知动点M(x,y)到定点A(0,4)的距离与到定直线y= -4的距离相等,请写出动点M形成的抛物线的解析式。
(2)若(1)中求得的抛物线与一次函数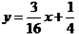 相交于B、C两点,求△OBC的面积。
相交于B、C两点,求△OBC的面积。
(3)若点D的坐标是(1,8),在(1)中求得的抛物线上是否存在点P,使得PA+PD最短?若存在,求出点P的坐标,若不存在,请说明理由。
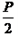 )的距离与它到定直线y= -
)的距离与它到定直线y= -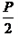 的距离相等,那么动点M形成的图形就是抛物线
的距离相等,那么动点M形成的图形就是抛物线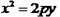 (p>0),如图。
(p>0),如图。(1)已知动点M(x,y)到定点A(0,4)的距离与到定直线y= -4的距离相等,请写出动点M形成的抛物线的解析式。
(2)若(1)中求得的抛物线与一次函数
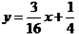 相交于B、C两点,求△OBC的面积。
相交于B、C两点,求△OBC的面积。(3)若点D的坐标是(1,8),在(1)中求得的抛物线上是否存在点P,使得PA+PD最短?若存在,求出点P的坐标,若不存在,请说明理由。
解:(1)根据定义可知: =4,p=8,
=4,p=8,
故抛物线的解析式为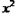 = 16y
= 16y

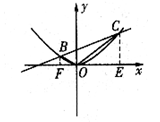
(2)画出简略示意图如图所示

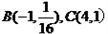 ∴
∴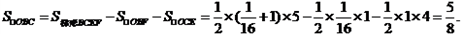
分别过点B、C作BF⊥x轴于F,CE⊥x轴于E
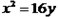 则
则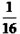
(3)存在
理由:画简略示意图如图所示,
设点P到直线y= -4的距离为d,
由抛物线的定义可知:PA =d,
则PA+ PD=d+PD,
∴过点D作直线y= -4的垂线段,与抛物线的交点即为P点
将x=1代入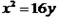 中,求得点直d
中,求得点直d
P(1,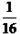 ),
),
∴抛物线上存在点P(1,去),使得PA+ PD最短。
 =4,p=8,
=4,p=8, 故抛物线的解析式为
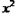 = 16y
= 16y
(2)画出简略示意图如图所示

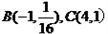 ∴
∴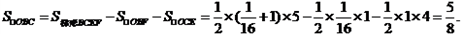
分别过点B、C作BF⊥x轴于F,CE⊥x轴于E
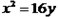 则
则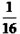

(3)存在
理由:画简略示意图如图所示,
设点P到直线y= -4的距离为d,
由抛物线的定义可知:PA =d,
则PA+ PD=d+PD,
∴过点D作直线y= -4的垂线段,与抛物线的交点即为P点
将x=1代入
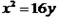 中,求得点直d
中,求得点直d P(1,
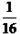 ),
), ∴抛物线上存在点P(1,去),使得PA+ PD最短。


练习册系列答案
相关题目
 的解(x,y)作为点的坐标,所确定的点就是直线和抛物线的公共点,如果直线L:x+my+n=0过点M(1,0),且直线L与抛物线C有且只有一个公共点,求相应的m,n的值.
的解(x,y)作为点的坐标,所确定的点就是直线和抛物线的公共点,如果直线L:x+my+n=0过点M(1,0),且直线L与抛物线C有且只有一个公共点,求相应的m,n的值. 的解(x,y)作为点的坐标,所确定的点就是直线和抛物线的公共点,如果直线L:x+my+n=0过点M(1,0),且直线L与抛物线C有且只有一个公共点,求相应的m,n的值.
的解(x,y)作为点的坐标,所确定的点就是直线和抛物线的公共点,如果直线L:x+my+n=0过点M(1,0),且直线L与抛物线C有且只有一个公共点,求相应的m,n的值.