题目内容
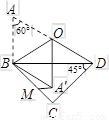
如图,一副三角板拼在一起,O为AD的中点,AB = a.将△ABO沿BO对折于△A′BO,
M为BC上一动点,则A′M的最小值为 .

【答案】

【解析】解:由折叠的性质知:AB=A′B=a,∠ABO=∠A′BO;
∵O是Rt△ABD斜边AD的中点,
∴OA=OB,即△ABO是等边三角形;
∴∠ABO=∠A′BO=60°;
∵∠ABD=90°,∠CBD=45°,
∴∠ABC=∠ABD+∠CBD=135°,
∴∠A′BM=135°-120°=15°;
易知当A′M⊥BC时,A′M最短;
过M作MH⊥A′B于H,取A′B的中点N,连接MN,如图;

在Rt△A′BM中,N是斜边A′B的中点,则BN=NM=A′N= ,∠B=∠NMB=15°;
,∠B=∠NMB=15°;
∴∠A′NM=30°;
 ,
,
 ,
,
 ,
,
由勾股定理得:


练习册系列答案
相关题目
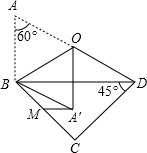 如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为
如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为