题目内容
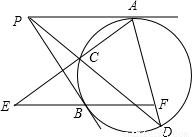
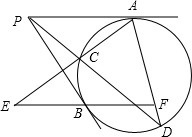如图，过圆外一点P作圆的两条切线PA、PB，A、B为切点，再过点P作圆的一条割线分别交圆于点C、D，过点B作PA的平行线分别交直线AC、AD于点E、F．求证：BE=BF．
分析：连接BC、BA、BD．由圆的切线、割线定理、弦切角定理、平行线的性质可得∠ABC=∠PAC=∠E，则推出△ABC∽△AEB，得出相关边的比，然后可得∠ABF=∠PAB=∠ADB，所以△ABF∽△ADB，得出相关边的比，结合切线定理可得结论．
解答：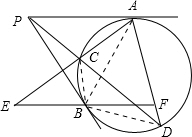
证明：如图，连接BC、BA、BD．所以∠ABC=∠PAC=∠E，则△ABC∽△AEB．
从而，
=
，即BE=
=AB•
①，
∵PA∥EF，PA是圆的切线，
∴∠ABF=∠PAB=∠ADB，
∴△ABF∽△ADB，从而
=
，
即BF=
=AB•
②，
另一方面，又因△PBC∽△PDB，△PCA∽△PAD，
∴
=
，
=
．
∵PA、PB是过圆外一点P作的圆的两条切线，
∴PA=PB，
∴
=
，于是
=
③，
∴由式①、②、③即知BE=BF．
证明：如图，连接BC、BA、BD．所以∠ABC=∠PAC=∠E，则△ABC∽△AEB．从而，
| BE |
| BC |
| AB |
| AC |
| AB•BC |
| AC |
| BC |
| AC |
∵PA∥EF，PA是圆的切线，
∴∠ABF=∠PAB=∠ADB，
∴△ABF∽△ADB，从而
| BF |
| BD |
| AB |
| AD |
即BF=
| AB•BD |
| AD |
| BD |
| AD |
另一方面，又因△PBC∽△PDB，△PCA∽△PAD，
∴
| BC |
| BD |
| PC |
| PB |
| AC |
| AD |
| PC |
| PA |
∵PA、PB是过圆外一点P作的圆的两条切线，
∴PA=PB，
∴
| BC |
| BD |
| AC |
| AD |
| BC |
| AC |
| BD |
| AD |
∴由式①、②、③即知BE=BF．
点评：本题主要考查相似三角形的判定和性质定理、圆的切线、割线定理、弦切角定理、平行线的性质，本题的关键在于根据弦切角定理、平行线的性质求出角的相等关系，得出相似三角形，求出比例关系．
练习册系列答案
相关题目
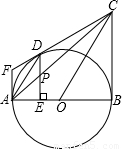
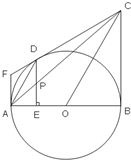24、如图所示：过圆外一点F作⊙O的两条切线FA、FD，AB是⊙O的直径，过O作OC∥AD，交FD的延长线于C，连CB，
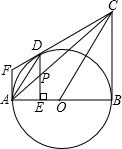如图所示：过圆外一点F作⊙O的两条切线FA、FD，AB是⊙O的直径，过O作OC∥AD，交FD的延长线于C，连CB，
