题目内容
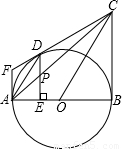
 24、如图所示:过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,过O作OC∥AD,交FD的延长线于C,连CB,
24、如图所示:过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,过O作OC∥AD,交FD的延长线于C,连CB,(1)求证:CB是⊙O的切线;
(2)过D点作DE⊥AB于E,交AC于P,求证:DP=PE.
分析:(1)根据已知得出BO=DO,CO=OC,以及∠DOC=∠COB,可得证明△CDO≌△CBO,即可证出;
(2)由切线长定理、相似关系或平行线分线段成比例定理,利用比例关系式求解.
(2)由切线长定理、相似关系或平行线分线段成比例定理,利用比例关系式求解.
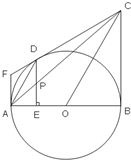
解答: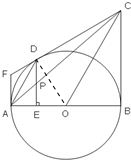 证明:(1)连接DO,∵过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,
证明:(1)连接DO,∵过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,
∴DO⊥CF,
∵OC∥AD,
∴∠DOC=∠ADO,∠COB=∠ODA,
∵AO=OD,
∴∠OAD=∠ODA,
∴∠DOC=∠COB,
∵BO=DO,CO=OC,
∴△CDO≌△CBO,
∴∠CDO=∠CBO=90°,
∴CB是⊙O的切线;
(2)证明:由切线长定理定理,
可设FA=FD=a,CD=CB=b(切线长定理),则CF=a+b,
∵FA∥DE,所以DP:FA=CD:CF,
即DP:a=b:(a+b),
∴DP=ab/(a+b);
∵DE∥BC,所以PE:BC=AP:AC=DF:CF,
即PE:b=a:(a+b),
∴PE=ab/(a+b);
∴DP=PE.
 证明:(1)连接DO,∵过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,
证明:(1)连接DO,∵过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,∴DO⊥CF,
∵OC∥AD,
∴∠DOC=∠ADO,∠COB=∠ODA,
∵AO=OD,
∴∠OAD=∠ODA,
∴∠DOC=∠COB,
∵BO=DO,CO=OC,
∴△CDO≌△CBO,
∴∠CDO=∠CBO=90°,
∴CB是⊙O的切线;
(2)证明:由切线长定理定理,
可设FA=FD=a,CD=CB=b(切线长定理),则CF=a+b,
∵FA∥DE,所以DP:FA=CD:CF,
即DP:a=b:(a+b),
∴DP=ab/(a+b);
∵DE∥BC,所以PE:BC=AP:AC=DF:CF,
即PE:b=a:(a+b),
∴PE=ab/(a+b);
∴DP=PE.
点评:此题主要考查了切线的判定定理以及平行线分线段成比例定理和切线长定理等知识,切线的性质定理与判定定理是中考中重点题型同学们应熟练掌握.

练习册系列答案
相关题目
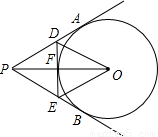
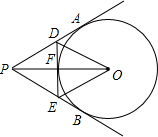 如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.
如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.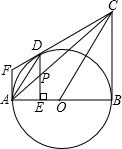 如图所示:过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,过O作OC∥AD,交FD的延长线于C,连CB,
如图所示:过圆外一点F作⊙O的两条切线FA、FD,AB是⊙O的直径,过O作OC∥AD,交FD的延长线于C,连CB,