题目内容
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l2于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l2于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 . 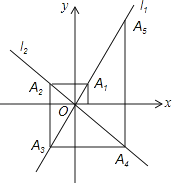
【答案】(21008 , 21009)
【解析】解:观察,发现规律:A1(1,2),A2(﹣2,2),A3(﹣2,﹣4),A4(4,﹣4),A5(4,8),…,
∴A2n+1((﹣2)n , 2(﹣2)n)(n为自然数).
∵2017=1008×2+1,
∴A2017的坐标为((﹣2)1008 , 2(﹣2)1008)=(21008 , 21009).
故答案为:(21008 , 21009).
写出部分An点的坐标,根据坐标的变化找出变化规律“A2n+1((﹣2)n , 2(﹣2)n)(n为自然数)”,依此规律即可得出结论.本题考查了一次函数图象上点的坐标特征以及规律型中坐标的变化,解题的关键是找出变化规律“A2n+1((﹣2)n , 2(﹣2)n)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,写出部分An点的坐标,根据坐标的变化找出变化规律是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下面是淄博市2016年4月份的天气情况统计表:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 多云 | 阴 | 多云 | 晴 | 多云 | 阴 | 晴 | 晴 | 晴 | 多云 | 多云 | 多云 | 晴 | 晴 | 雨 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 雨 | 多云 | 多云 | 多云 | 多云 | 晴 | 多云 | 多云 | 晴 | 多云 | 多云 | 多云 | 晴 | 晴 | 晴 |
(1)请完成下面的汇总表:
天气 | 晴 | 多云 | 阴 | 雨 |
天数 |
(2)根据汇总表绘制条形图;
(3)在该月中任取一天,计算该天多云的概率.
【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?