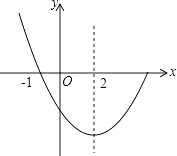题目内容
【题目】如图，抛物线y=x2+bx+c与x轴相交于A、B两点，点B的坐标为（3，0），与y轴相交于点C（0，﹣3），顶点为D．
（1）求出抛物线y=x2+bx+c的表达式；
（2）连结BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m．
①当m为何值时，四边形PEDF为平行四边形．
②设四边形OBFC的面积为S，求S的最大值．
【答案】
（1）
解：∵抛物线过B、C两点，
∴ 
，解得 
，
∴抛物线表达式为y=x2﹣2x﹣3
（2）
解：①∵B（3，0），C（0，﹣3），
∴直线BC解析式为y=x﹣3，
∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴D（1，﹣4），
∴E（1，﹣2），
∴DE=﹣2﹣（﹣4）=2，
∵PF∥DE，且P（m，m﹣3），
∴F（m，m2﹣2m﹣3），
∵点P为线段BC上的一个动点，
∴PF=m﹣3﹣（m2﹣2m﹣3）=﹣m2+3m，
当四边形PEDF为平行四边形时，则有PF=DE=2，
即﹣m2+3m=2，解得m=1（舍去）或m=2，
∴当m的值为2时，四边形PEDF为平行四边形；②由①可知PF=﹣m2+3m，
∴S△FBC= 
PFOB= ×3（﹣m2+3m）=﹣ 
（m﹣ ）2+ 
，
∵S△OBC= OBOC= ×3×3= 
，
∴S=S△FBC+S△OBC=﹣ （m﹣ ）2+ + =﹣ （m﹣ ）2+ 
，
∵﹣ ＜0，
∴当m= 时，S有最大值
【解析】（1）由B、C两点的坐标，利用待定系数法可求得抛物线的表达式；（2）①可求得直线BC的解析式，则可表示出P、F的坐标，从而可表示出PF和DE的长，由平行四边形的性质可知PF=DE，则可得到关于m的方程，可求得m的值；②用m可表示出PF的长，则可表示出△BCF的面积，从而可表示出四边形OBFC的面积，利用二次函数的性质可求得其最大值．
