题目内容
【题目】已知x，y，z是三个非负数，并且满足x+2y-5z=6，2x+y+5z=9．设k=3x+y+5z，记a为k的最大值，b为k的最小值，试求ab的值．
【答案】117
【解析】
首先把x+2y-5z=6，2x+y+5z=9，组成方程组，分别用含z的代数式表示x和y，根据x，y，z是三个非负数求出z的取值范围，再把x和y代入k=3x+y+5z中，可得到k=-5z+13，求出k的最大值和最小值，即可以得到答案．
解：联立方程组
，解得
，
∵x，y，z是非负数，
∴
，
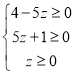解不等式组得0≤z≤
，
把 代入k=3x+y+5z，得 k=3(4-5z)+5z+1+5z=-5z+13，
则当z=0时，k有最大值a＝13，当z= 时，k有最小值b=9，
此时 ab=13×9=117．
练习册系列答案
阅读快车系列答案
相关题目
