题目内容
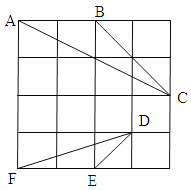
【题目】如图,在4×4的正方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC , BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
【答案】(1)![]() ,
, ![]() ; (2)相似,证明见解析.
; (2)相似,证明见解析.
【解析】试题分析:(1)先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△ACH中利用勾股定理即可求出AC的长;
(2)根据相似三角形的判定定理,夹角相等,对应边成比例即可证明△ABC与△DEF相似.
试题解析:(1)∵△BCG是等腰直角三角形,∴∠GBC=45°,∵∠ABG=90°,∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△AHC中,AH=4,CH=2,∴AC=![]() =
=![]() =
=![]() .
.
故答案为:135, ![]() ;
;
(2)△ABC∽△DEF.
证明:∵在4×4的正方形方格中,∠ABC=∠DEF=135°,∴∠ABC=∠DEF.
∵AB=2,BC=![]() ,FE=2,DE=
,FE=2,DE=![]() ,∴
,∴![]() =
=![]() ,
, ![]() =
=![]() ,∴
,∴![]() ,∴△ABC∽△DEF.
,∴△ABC∽△DEF.

练习册系列答案
相关题目
【题目】标枪飞行的路线是一条抛物线,不考虑空气阻力,标枪距离地面的高度h(单位:m)与标枪被掷出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①标枪距离地面的最大高度大于20m;②标枪飞行路线的对称轴是直线t=![]() ;③标枪被掷出9s时落地;④标枪被掷出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
;③标枪被掷出9s时落地;④标枪被掷出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4