题目内容
【题目】如图3,在□ABCD中,点E、F在对角线AC上,且AE=CF . 请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并说明它和图中已知的某一线段相等(只需说明一组线段相等即可).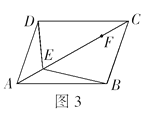
(1)连接 .
(2)猜想:= .
(3)试说明理由.
【答案】
(1)BF或DF
(2)BF或DF;DE或 BE
(3)
理由:BF=DE时
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE=CF
∴△ADE≌△CBF,
∴BF=DE.
DF=BE时,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF
∴△ABE≌△CDF,
∴BE=DF.
【解析】(1)因为一点F已经确定,另一点只能从A、B、C、D、E、在选择,而A、C、E都已和F点连接,只有再连接BF或DF.(2)连接BF时,填BF=DE;连接DF时,填DF=BE
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目