题目内容
如图所示，点A、B在直线MN上，AB=11cm，⊙A、⊙B的半径均为1cm，⊙A以每秒2cm的速度自左向右运动，与此同时，⊙A的半径也不断增大，其半径r（cm）与时间t（秒）之间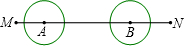
的关系式为r=1+t（t≥0），当点A出发后分析：根据两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
解答：解：分四种情况考虑：
①当首次外切时，有2t+1+1+t=11，解得：t=3；
②当首次内切时，有2t+1+t-1=11，解得：t=
；
③当再次内切时，有2t-（1+t-1）=11，解得：t=11；
④当再次外切时，有2t-（1+t）-1=11，解得：t=13．
∴当点A出发后3、
、11、13秒两圆相切．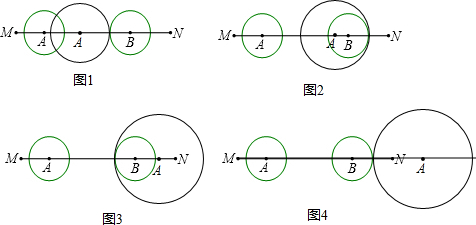
①当首次外切时，有2t+1+1+t=11，解得：t=3；
②当首次内切时，有2t+1+t-1=11，解得：t=
| 11 |
| 3 |
③当再次内切时，有2t-（1+t-1）=11，解得：t=11；
④当再次外切时，有2t-（1+t）-1=11，解得：t=13．
∴当点A出发后3、
| 11 |
| 3 |
点评：本题考查了两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
练习册系列答案
相关题目
13、如图所示，点A、B在直线l的同侧，AB=4cm，点C是点B关于直线l的对称点，AC交直线l于点D，AC=5cm，则△ABD的周长为
23、如图所示，点C、F在BE上，∠1=∠2，BC=EF，请补充条件：
41、如图所示，点E，F在正方形ABCD的边BC，CD上，AE，BF相交于点G，BE=CF，求证：（1）AE=BF；（2）AE⊥BF．
两个反比例函数