题目内容
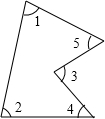 如图,∠1=65°,∠2=85°,∠3=60°,∠4=40°,则∠5=
如图,∠1=65°,∠2=85°,∠3=60°,∠4=40°,则∠5=
- A.45°
- B.50°
- C.55°
- D.60°
B
分析:通过作如图所示的辅助线将∠3变为一个三角形的内角,根据三角形的内角和是180°,可得∠ECB+∠EBC的值,再根据四边形ABCD的内角和等于360°,并将∠ECB+∠EBC的值整体代入,可得∠5的度数.
解答: 解:如图,连接BC,
解:如图,连接BC,
在△EBC中,∠3+∠ECB+∠EBC=180°,
∴∠ECB+∠EBC=180°-∠3=180°-60°=120°.
在四边形ABCD中,∠1+∠2+∠4+∠EBC+∠ECB+∠5=360°,
∴∠5=360-∠1-∠2-∠4-(∠EBC+∠ECB)=360°-65°-85°-40°-120°=50°.
故选B.
点评:本题考查三角形与四边形的内角和以及整体代入思想.
分析:通过作如图所示的辅助线将∠3变为一个三角形的内角,根据三角形的内角和是180°,可得∠ECB+∠EBC的值,再根据四边形ABCD的内角和等于360°,并将∠ECB+∠EBC的值整体代入,可得∠5的度数.
解答:
 解:如图,连接BC,
解:如图,连接BC,在△EBC中,∠3+∠ECB+∠EBC=180°,
∴∠ECB+∠EBC=180°-∠3=180°-60°=120°.
在四边形ABCD中,∠1+∠2+∠4+∠EBC+∠ECB+∠5=360°,
∴∠5=360-∠1-∠2-∠4-(∠EBC+∠ECB)=360°-65°-85°-40°-120°=50°.
故选B.
点评:本题考查三角形与四边形的内角和以及整体代入思想.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
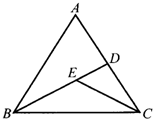 24、如图,∠A=65°,∠ABD=∠DCE=30°,求∠BEC的度数.
24、如图,∠A=65°,∠ABD=∠DCE=30°,求∠BEC的度数.
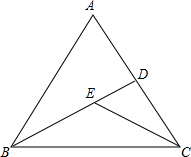 如图:∠A=65°,∠ABD=∠DCE=30°,且CE平分∠ACB,求∠BEC的度数.
如图:∠A=65°,∠ABD=∠DCE=30°,且CE平分∠ACB,求∠BEC的度数.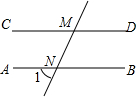 如图,∠1=65°,∠DMN=115°,求证:CD∥AB.
如图,∠1=65°,∠DMN=115°,求证:CD∥AB.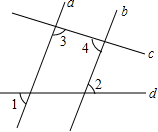 如图,∠1=65°,∠2=65°,∠3=95°
如图,∠1=65°,∠2=65°,∠3=95°