题目内容
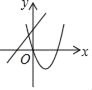
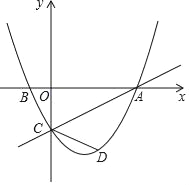
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点A,与y轴交于点C,抛物线y=
x﹣2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
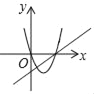
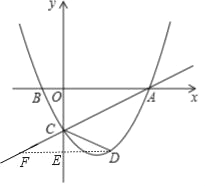
(2)点D为直线AC下方抛物线上一点,且∠ACD=2∠BAC,求点D的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)D(2,﹣3)
x﹣2;(2)D(2,﹣3)
【解析】
(1)求出A、C两点坐标,利用待定系数法即可解决问题;
(2)过点D作DF∥x轴,交y轴于点E,则∠CFD=∠BAC,推出∠CDF=∠CFD,可得∠ACD=2∠BAC,由此利用三角函数构建方程即可解决问题;
解:(1)直线y=![]() x﹣2与x轴交于点A, 与y轴交于点C,x=0时,y=-2,y=0时,x=4,所以A(4,0),C(0,﹣2),
x﹣2与x轴交于点A, 与y轴交于点C,x=0时,y=-2,y=0时,x=4,所以A(4,0),C(0,﹣2),
把A(4,0),C(0,-2)代入y=![]() x2+bx+c,得到
x2+bx+c,得到![]() ,
,
解得 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
(2)过点D作DF∥x轴,交y轴于点E,则∠CFD=∠BAC,
∵∠ACD=2∠BAC=∠CFD+∠CDF,
∴∠CDF=∠CFD,
∴tan∠CDF=tan∠BAC=![]() ,
,
∴![]()
解得x=2,
∴D(2,﹣3).

练习册系列答案
相关题目