题目内容
如图,已知半径为1的⊙O1与x轴交于A、B两点,经过原点的直线MN切⊙O1于点M,圆心O1的坐标为(2,0).
(1)求切线MN的函数解析式;
(2)线段OM上是否存在一点P,使得以P、O、A为顶点的三角形与△OO1M相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)若将⊙O1沿着x轴的负方向以每秒1个单位的速度移动;同时将直线MN以每秒2个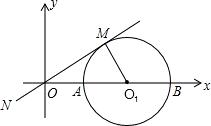 单位的速度向下平移,设运动时间为t(t>0),求t为何值时,直线MN再一次与⊙O1相切?(本小题保留3位有效数字)
单位的速度向下平移,设运动时间为t(t>0),求t为何值时,直线MN再一次与⊙O1相切?(本小题保留3位有效数字)
解:(1)过点M作MF⊥x轴,垂足为F
∵MN是切线,M为切点,
∴O1M⊥OM
在Rt△OO1M中,
∴∠O1OM=30°,
在Rt△MOF中,∠O1OM=30°,
∴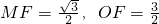
∴点M坐标为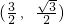 (2分)
(2分)
设切线MN的函数解析式为y=kx(k≠0),由题意可知 ,
,
解得:
∴切线MN的函数解析式为 (1分)
(1分)

(2)存在.
①过点A作AP1⊥x轴,与OM交于点P1.
可得Rt△AP1O∽Rt△MO1O,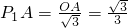 ,
,
∴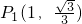 (2分)
(2分)
②过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H.
可得Rt△AP2O∽Rt△O1MO
在Rt△OP2A中,∵OA=1,
∴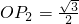
在Rt△OP2H中,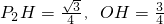 ,
,
∴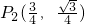 (2分)
(2分)
∴符合条件的P点坐标有 ,
,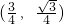
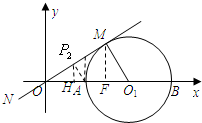
(3)如图,作MF⊥x轴于点F,
在Rt△OFM中,OF=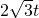 ;
;
在Rt△O1MF中,O1F=2 t-(2-t)
t-(2-t)
∵O1F=2O1M=2,
∴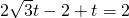 ,
,
解得: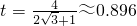 .
.

分析:过点M作MF⊥x轴,垂足为F,根据MN是切线,M为切点,得到O1M⊥OM,在Rt△OO1M中根据正弦值的定义求得∠O1OM=30°,从而求得MF和OF,最后求得点M的坐标后利用待定系数法求得直线的解析式即可.
(2)过点A作AP1⊥x轴,与OM交于点P1.利用Rt△AP1O∽Rt△MO1O求得P1A后即可求得点P1的坐标;过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H.
利用Rt△AP2O∽Rt△O1MO求得OP2和OH即可求得P2的坐标;
(3)首先Rt△OCD中求得OC=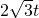 ;然后在Rt△O1MC中,求得O1C=2
;然后在Rt△O1MC中,求得O1C=2 t-(2-t,然后根据O1C=2O1M=2列出有关t的方程
t-(2-t,然后根据O1C=2O1M=2列出有关t的方程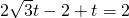 即可求得t值.
即可求得t值.
点评:本题是直线与圆的方程综合性题,对于存在性的处理方法,先假设存在再由题意用设而不求思想和韦达定理列出关系式,注意验证所求值的范围.
∵MN是切线,M为切点,
∴O1M⊥OM
在Rt△OO1M中,

∴∠O1OM=30°,

在Rt△MOF中,∠O1OM=30°,

∴
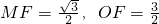
∴点M坐标为
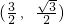 (2分)
(2分)设切线MN的函数解析式为y=kx(k≠0),由题意可知
 ,
,解得:

∴切线MN的函数解析式为
 (1分)
(1分)
(2)存在.
①过点A作AP1⊥x轴,与OM交于点P1.
可得Rt△AP1O∽Rt△MO1O,
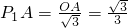 ,
,∴
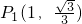 (2分)
(2分)②过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H.
可得Rt△AP2O∽Rt△O1MO
在Rt△OP2A中,∵OA=1,
∴
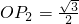
在Rt△OP2H中,
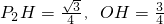 ,
,∴
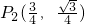 (2分)
(2分)∴符合条件的P点坐标有
 ,
,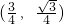
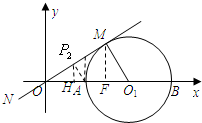
(3)如图,作MF⊥x轴于点F,
在Rt△OFM中,OF=
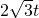 ;
;在Rt△O1MF中,O1F=2
 t-(2-t)
t-(2-t)∵O1F=2O1M=2,
∴
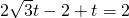 ,
,解得:
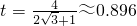 .
.
分析:过点M作MF⊥x轴,垂足为F,根据MN是切线,M为切点,得到O1M⊥OM,在Rt△OO1M中根据正弦值的定义求得∠O1OM=30°,从而求得MF和OF,最后求得点M的坐标后利用待定系数法求得直线的解析式即可.
(2)过点A作AP1⊥x轴,与OM交于点P1.利用Rt△AP1O∽Rt△MO1O求得P1A后即可求得点P1的坐标;过点A作AP2⊥OM,垂足为P2,过P2点作P2H⊥OA,垂足为H.
利用Rt△AP2O∽Rt△O1MO求得OP2和OH即可求得P2的坐标;
(3)首先Rt△OCD中求得OC=
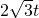 ;然后在Rt△O1MC中,求得O1C=2
;然后在Rt△O1MC中,求得O1C=2 t-(2-t,然后根据O1C=2O1M=2列出有关t的方程
t-(2-t,然后根据O1C=2O1M=2列出有关t的方程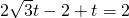 即可求得t值.
即可求得t值.点评:本题是直线与圆的方程综合性题,对于存在性的处理方法,先假设存在再由题意用设而不求思想和韦达定理列出关系式,注意验证所求值的范围.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目

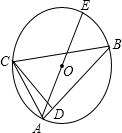
 如图,已知半径为1的⊙O1与x轴交于A,B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.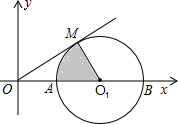 如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.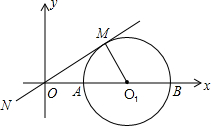 单位的速度向下平移,设运动时间为t(t>0),求t为何值时,直线MN再一次与⊙O1相切?(本小题保留3位有效数字)
单位的速度向下平移,设运动时间为t(t>0),求t为何值时,直线MN再一次与⊙O1相切?(本小题保留3位有效数字)