题目内容
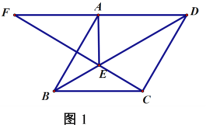
【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
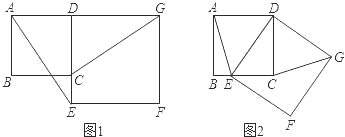
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
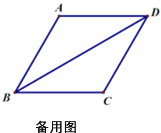
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
【答案】(1)AE⊥CE,证明见解析;(2)成立,证明见解析
【解析】
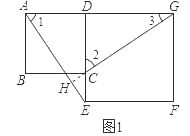
试题(1)观察图形,AE、CG的位置关系可能是垂直,下面着手证明.由于四边形ABCD、DEFG都是正方形,易证得△ADE≌△CDG,则∠1=∠2,由于∠2、∠3互余,所以∠1、∠3互余,由此可得AH⊥CG.
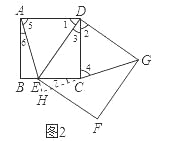
(2)题(1)的结论仍然成立,参照(1)题的解题方法,可证△ADE≌△CDG,得∠5=∠4,由于∠4、∠7互余,而∠5、∠6互余,那么∠6=∠7;由图知∠AEB=∠CEH=90°-∠6,即∠7+∠CEH=90°,由此得证.
试题解析:(1)AE⊥GC;
证明:延长GC交AE于点H,
在正方形ABCD与正方形DEFG中,
AD=DC,∠ADE=∠CDG=90°,
DE=DG,
∴△ADE≌△CDG,
∴∠1=∠2;
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠AHG=180°-(∠1+∠3)=180°-90°=90°,
∴AE⊥GC.
(2)成立;
证明:延长AE和GC相交于点H,
在正方形ABCD和正方形DEFG中,
AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,
∴∠1=∠2=90°-∠3;
∴△ADE≌△CDG,
∴∠5=∠4;
又∵∠5+∠6=90°,∠4+∠7=180°-∠DCE=180°-90°=90°,
∴∠6=∠7,
又∵∠6+∠AEB=90°,∠AEB=∠CEH,
∴∠CEH+∠7=90°,
∴∠EHC=90°,
∴AE⊥GC.

 阅读快车系列答案
阅读快车系列答案