题目内容
【题目】已知函数y=![]() +b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
+b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量x的取值范围;
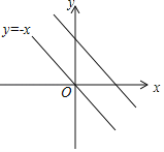
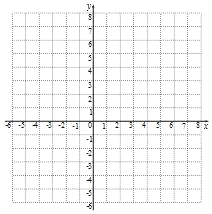
(2)请在下列直角坐标系中画出该函数的图象;
(3)请你在上方直角坐标系中画出函数y=2x的图象,结合上述函数的图象,写出不等式![]() +b≤2x的解集.
+b≤2x的解集.
【答案】(1)y=![]() +2(x≠1);(2)见解析;(3)图象见解析;x≥2或0≤x<1;.
+2(x≠1);(2)见解析;(3)图象见解析;x≥2或0≤x<1;.
【解析】
(1)分别把两组数代入y=![]() +b得到方程组,求出a,b即可;
+b得到方程组,求出a,b即可;
(2)利用描点法画出图象即可;
(3)利用图象即可解决问题.
解:(1)把x=2时,y=4;x=﹣1时,y=1代入y=![]() +b得
+b得
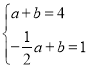 ,
,
解得![]() ,
,
∴该函数的解析式为y=![]() +2(x≠1);
+2(x≠1);
(2)如图:
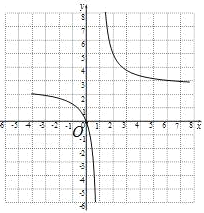
(3)如图:在平面直角坐标系中作直线y=2x,
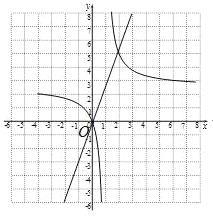
![]() 的图象与直线y=2x的交点为(0,0),(2,4),结合函数图象可得
的图象与直线y=2x的交点为(0,0),(2,4),结合函数图象可得![]() 的解集为x≥2或0≤x<1。
的解集为x≥2或0≤x<1。
故答案为:x≥2或0≤x<1

练习册系列答案
相关题目