题目内容
(2011•嘉定区一模)在正方形ABCD中,已知AB=6,点E在边CD上,且DE:CE=1:2,如图.点F在CB的延长线上,如果△ADE与点C、E、F所组成的三角形相似,那么CF= .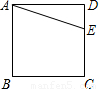
【答案】分析:首先由四边形ABCD是正方形,可得∠D=∠C=90°,AD=DC=AB=6;又由DE:CE=1:2,可求得DE与EC的长;再从△ADE∽△ECF与△ADE∽△FCE入手分析,利用相似三角形的对应边成比例,即可求得CF的长.
解答: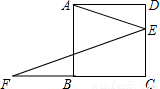 解:如图:
解:如图:
∵四边形ABCD是正方形,AB=6,
∴∠D=∠C=90°,AD=DC=AB=6,
∵DE:CE=1:2,
∴DE=2,CE=4;
∵△ADE∽△FCE,
∴ ,
,
∴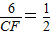 ,
,
∴CF=12.
故答案为:12.
点评:此题考查了相似三角形的判定与性质与正方形的性质.注意此题的答案不唯一,解题的时候小心别漏解.
解答:
 解:如图:
解:如图:∵四边形ABCD是正方形,AB=6,
∴∠D=∠C=90°,AD=DC=AB=6,
∵DE:CE=1:2,
∴DE=2,CE=4;
∵△ADE∽△FCE,
∴
 ,
,∴
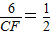 ,
,∴CF=12.
故答案为:12.
点评:此题考查了相似三角形的判定与性质与正方形的性质.注意此题的答案不唯一,解题的时候小心别漏解.

练习册系列答案
相关题目
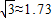 ,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,cot10°≈84.29.
,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,cot10°≈84.29.