题目内容
【题目】在平面直角坐标系xOy中,对于两个点P,Q和图形W,如果在图形W上存在点M,N(M,N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.
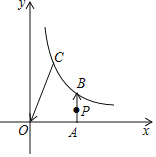
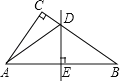
(1)如图1,已知点A(0,3),B(2,3).
①设点O与线段AB上一点的距离为d,则d的最小值是 ,最大值是 ;
②在P1(![]() ,0),P2(1,4),P3(﹣3,0)这三个点中,与点O是线段AB的一对平衡点的是
,0),P2(1,4),P3(﹣3,0)这三个点中,与点O是线段AB的一对平衡点的是
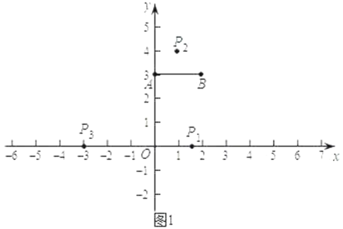
(2)如图2,已知圆O的半径为1,点D的坐标为(5,0),若点E(x,2)在第一象限,且点D与点E是圆O的一对平衡点,求x的取值范围.
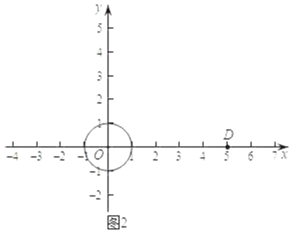
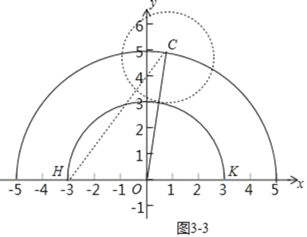
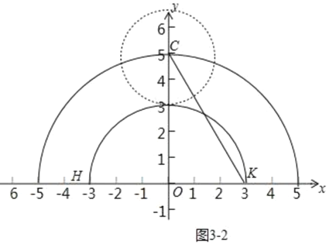
(3)如图3,已知点H(﹣3,0),以点O为圆心,OH长为半径画弧交x轴的正半轴于点K,点C(a,b)(其中b≥0)是坐标平面内一个动点,且OC=5,圆C是以点C为圆心,半径为2的圆,若弧HK上的任意两个点都是圆C的一对平衡点,直接写出b的取值范围.
【答案】(1)3,![]() ,P1;(2)满足条件的x的值为
,P1;(2)满足条件的x的值为![]() ≤x≤3
≤x≤3![]() ;(3)满足条件的b的值为
;(3)满足条件的b的值为![]() ≤b≤5.
≤b≤5.
【解析】
(1)①观察图象d的最小值是OA长,最大值是OB长,由勾股定理得出结果;②由题意知P1;
(2)如图,可得OE1=3,解得此时x=![]() ,OE2=7,解得x=3
,OE2=7,解得x=3![]() ,可求出范围;
,可求出范围;
(3)由点C在以O为圆心5为半径的上半圆上运动,推出以C为圆心2为半径的圆刚好与弧HK相切,此时要想弧HK上任意两点都是圆C的平衡点,需要满足CK≤6,CH≤6,分两种情形分别求出b的值即可判断.
(1)①由题意知:OA=3,OB=![]() ,则d的最小值是3,最大值是
,则d的最小值是3,最大值是![]() ;
;
②根据平衡点的定义,点P1与点O是线段AB的一对平衡点,
故答案为3,![]() ,P1.
,P1.
(2)如图2中,
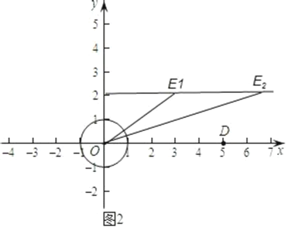
由题意点D到⊙O的最近距离是4,最远距离是6,
∵点D与点E是⊙O的一对平衡点,此时需要满足E1到⊙O的最大距离是4,即OE1=3,可得x=![]()
同理:当E2到⊙的最小距离为是6时,OE2=7,此时x=![]()
综上所述,满足条件的x的值为![]()
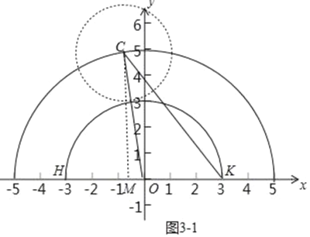
(3)∵点C在以O为圆心5为半径的上半圆上运动,
∴以C为圆心2为半径的圆刚好与弧HK相切,此时要想弧HK上任意两点都是圆C的平衡点,需要满足CK≤6,CH≤6,
如图3﹣1中,当CK=6时,作CM⊥HK于H.
由题意: 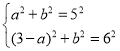
解得: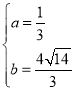 或
或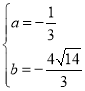 (舍弃),
(舍弃),
如图3﹣3中,当CH=6时,同法可得![]()
在两者中间时,a=0,b=5,
观察图象可知:满足条件的b的值为![]()

 阅读快车系列答案
阅读快车系列答案