题目内容
如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积
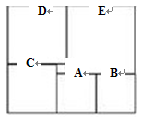
解:设正方形A的边长为x厘米,则
正方形B的边长为_______ 厘米,
正方形C的边长为_______ 厘米
正方形D的边长为_______ 厘米,
正方形E的边长为_______ 厘米。
由题意可得方程:
解得 x=
答:长方形的面积为________ 平方厘米。

解:设正方形A的边长为x厘米,则
正方形B的边长为_______ 厘米,
正方形C的边长为_______ 厘米
正方形D的边长为_______ 厘米,
正方形E的边长为_______ 厘米。
由题意可得方程:
解得 x=
答:长方形的面积为________ 平方厘米。
x,x+1,x+2,x+3(或2x-1);x=4;143.
解:设正方形A的边长为x厘米,则
正方形B的边长为 x 厘米,
正方形C的边长为 (x+1)厘米,
正方形D的边长为 (x+2)厘米,
正方形E的边长为 (x+3)或(2x-1)厘米
由题意得:x+3=2x-1解得x=4,
∴大正方形的边长为11,13,
∴面积为11×13=143.
故答案为:x x+1 x+2 x+3(或2x-1);x=4;143.
依次得到各个正方形的边长,利用正方形E的边长的不同表达方式得到方程,求得A的边长,进而求得大长方形的边长,相乘即为所求的面积.
正方形B的边长为 x 厘米,
正方形C的边长为 (x+1)厘米,
正方形D的边长为 (x+2)厘米,
正方形E的边长为 (x+3)或(2x-1)厘米
由题意得:x+3=2x-1解得x=4,
∴大正方形的边长为11,13,
∴面积为11×13=143.
故答案为:x x+1 x+2 x+3(或2x-1);x=4;143.
依次得到各个正方形的边长,利用正方形E的边长的不同表达方式得到方程,求得A的边长,进而求得大长方形的边长,相乘即为所求的面积.

练习册系列答案
相关题目
 ,
,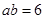 ,则
,则 ,
, 。
。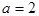 ,
,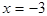 时,求
时,求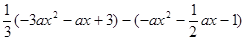 ;
;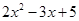 是 次 项式.
是 次 项式. (2)
(2)


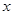 的二次三项式
的二次三项式