题目内容
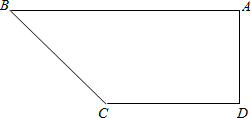 直角梯形ABCD中,AB∥CD,DA⊥AB,AB=26cm,CD=24cm,AD=8cm,有两个动点P和Q,点P在CD上,由D向C以每秒1cm的速度移动,点Q在AB上由B向A以每秒3cm的速度移动.
直角梯形ABCD中,AB∥CD,DA⊥AB,AB=26cm,CD=24cm,AD=8cm,有两个动点P和Q,点P在CD上,由D向C以每秒1cm的速度移动,点Q在AB上由B向A以每秒3cm的速度移动.
①问时间t经过几秒时,BCPQ为平行四边形?
②问时间t经过几秒时,BCPQ为等腰梯形?
③PQ与以AD为直径的圆O相切?相离?相交?
 解:①∵四边形BCPQ是平行四边形,
解:①∵四边形BCPQ是平行四边形,∴BQ=CP,
∴24-t=3t,
t=6,
答:时间t经过6秒时,BCPQ为平行四边形.
②解:过C作CN⊥AB于N,过P作PM⊥BQ于M,
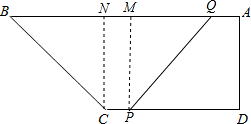
即∠BNC=∠PMQ=90°,CN∥PM,
∵AB∥CD,
∴四边形CNMP是平行四边形,
∴CN=PM,CP=MN,
∵四边形BCPQ是等腰梯形,
∴BC=PQ,∠B=∠BQP,
∵在△BCN和△QPM中
 ,
,∴△BCN≌△QPM,
∴BN=MQ=26-24=2,
即2+2+24-t=3t,
t=7,
答:时间t经过7秒时,BCPQ为等腰梯形.
③解:过P作PE⊥AB于E,
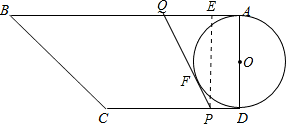
∵直角梯形ABCD,
∴∠A=∠D=90°,
∴BA切⊙O于A,CD切⊙O于D,
设PQ切⊙O于F,
∴由切线长定理得:QA=QF=26-3t,DP=PF=t
则PQ=26-3t+t=26-2t,
∵∠A=∠D=∠PEA=90°,
∴四边形PEAD是矩形,
∴AD=PE=8,AE=PD=t,
∴QE=26-3t-t=26-4t,
在Rt△PEQ中,由勾股定理得:PE2+QE2=PQ2,
即82+(26-4t)2=(26-2t)2,
解得:t1=8,t2=
 .
.∴当t是8秒或
 秒时,PQ与以AD为直径的圆O相切;当t<
秒时,PQ与以AD为直径的圆O相切;当t< 秒或t>8秒时,PQ与以AD为直径的圆O相交;当
秒或t>8秒时,PQ与以AD为直径的圆O相交;当 秒<t<8秒时,PQ与以AD为直径的圆O相离.
秒<t<8秒时,PQ与以AD为直径的圆O相离.分析:①根据平行四边形性质得出BQ=CP,代入得出方程24-t=3t,求出即可;
②过C作CN⊥AB于N,过P作PM⊥BQ于M,得出矩形CPMN,推出CN=PM,CP=MN,求出BN=MQ=2,根据BN+MN+QM=3t,代入求出即可;
③过P作PE⊥AB于E,得出矩形ADPE,推出AE=DP,AD=PE,根据切线长定理得长PQ=QA+PD=26-2t,在Rt△PEQ中,根据勾股定理得出一个关于t的方程,求出方程的解即可.
点评:本题考查了切线的性质和判定,切线长定理,勾股定理,平行四边形的性质,等腰梯形的性质,矩形的性质和判定,直线与圆的位置关系等知识点,主要考查学生综合运用定理进行推理和计算的能力,本题综合性比较强,难度偏大.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为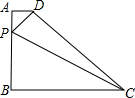 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为 下结论:
下结论: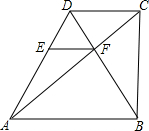 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.