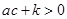题目内容
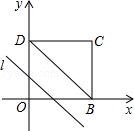
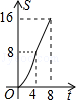
如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )
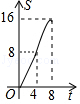
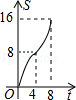

A B C D


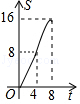


A B C D
D
试题分析:①当0≤t≤4时,S=
 ×t×t=
×t×t= t2,即S=
t2,即S= t2.
t2.该函数图象是开口向上的抛物线的一部分.
故B、C错误;
②当4<t≤8时,S=16﹣
 ×(t﹣4)×(t﹣4)=
×(t﹣4)×(t﹣4)= t2,即S=﹣
t2,即S=﹣ t2+4t+8.
t2+4t+8.该函数图象是开口向下的抛物线的一部分.
故A错误.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其图像抛物线交
,其图像抛物线交 轴的于点A(1,0)、B(3,0),交y轴于点C.直线
轴的于点A(1,0)、B(3,0),交y轴于点C.直线 过点C,且交抛物线于另一点E(点E不与点A、B重合).
过点C,且交抛物线于另一点E(点E不与点A、B重合). 经过抛物线顶点D,交
经过抛物线顶点D,交
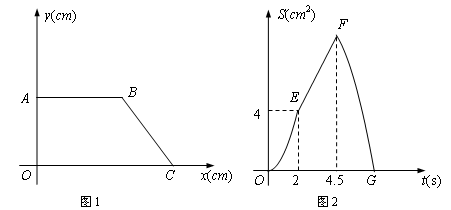
 ,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从点C出发,以1cm/s的速度沿边CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△CPQ的面积为S(cm2), 已知S与t之间的函数关系如图2中曲线段OE、线段EF与曲线段FG给出.
,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从点C出发,以1cm/s的速度沿边CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△CPQ的面积为S(cm2), 已知S与t之间的函数关系如图2中曲线段OE、线段EF与曲线段FG给出. ?
?


 与抛物线
与抛物线 的图象都经过
的图象都经过 轴上的D点,抛物线与
轴上的D点,抛物线与 轴交于A、B两点,其对称轴为直线
轴交于A、B两点,其对称轴为直线 ,且
,且 .直线
.直线 ; ②
; ② ; ③
; ③ ; ④
; ④ ; ⑤
; ⑤