题目内容
【题目】如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，﹣4）．
（1）求抛物线的解析式；
（2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，
①求当△BEF与△BAO相似时，E点坐标；
②记平移后抛物线与AB另一个交点为G，则S△EFG与S△ACD是否存在8倍的关系？若有请直接写出F点的坐标．
【答案】
（1）
解：直线AB的解析式为y=2x+4，
令x=0，得y=4；令y=0，得x=﹣2．
∴A（﹣2，0）、B（0，4）．
∵抛物线的顶点为点A（﹣2，0），
∴设抛物线的解析式为：y=a（x+2）2，
点C（0，﹣4）在抛物线上，代入上式得：﹣4=4a，解得a=﹣1，
∴抛物线的解析式为y=﹣（x+2）2
（2）
解：平移过程中，设点E的坐标为（m，2m+4），
则平移后抛物线的解析式为：y=﹣（x﹣m）2+2m+4，
∴F（0，﹣m2+2m+4）．
①∵点E为顶点，∴∠BEF≥90°，
∴若△BEF与△BAO相似，只能是点E作为直角顶点，
∴△BAO∽△BFE，
∴ 
，即 
，可得：BE=2EF．
如答图2﹣1，过点E作EH⊥y轴于点H，则点H坐标为：H（0，2m+4）．
∵B（0，4），H（0，2m+4），F（0，﹣m2+2m+4），
∴BH=|2m|，FH=|﹣m2|．
在Rt△BEF中，由射影定理得：BE2=BHBF，EF2=FHBF，
又∵BE=2EF，∴BH=4FH，
即：4|﹣m2|=|2m|．
若﹣4m2=2m，解得m=﹣ 
或m=0（与点B重合，舍去）；
若﹣4m2=﹣2m，解得m= 或m=0（与点B重合，舍去），此时点E位于第一象限，∠BEF为锐角，故此情形不成立．
∴m=﹣ ，
∴E（﹣ ，3）．
②假设存在．
联立抛物线：y=﹣（x+2）2与直线AB：y=2x+4，可求得：D（﹣4，﹣4），
∴S△ACD= ×4×4=8．
∵S△EFG与S△ACD存在8倍的关系，
∴S△EFG=64或S△EFG=1．
联立平移抛物线：y=﹣（x﹣m）2+2m+4与直线AB：y=2x+4，可求得：G（m﹣2，2m）．
∴点E与点G横坐标相差2，即：|xG|﹣|xE|=2．
当顶点E在y轴左侧时，如答图2﹣2，
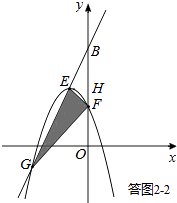
S△EFG=S△BFG﹣S△BEF= BF|xG|﹣ BF|xE|= BF（|xG|﹣|xE|）=BF．
∵B（0，4），F（0，﹣m2+2m+4），∴BF=|﹣m2+2m|．
∴|﹣m2+2m|=64或|﹣m2+2m|=1，
∴﹣m2+2m可取值为：64、﹣64、1、﹣1．
当取值为64时，一元二次方程﹣m2+2m=64无解，故﹣m2+2m≠64．
∴﹣m2+2m可取值为：﹣64、1、﹣1．
∵F（0，﹣m2+2m+4），
∴F坐标为：（0，﹣60）、（0，3）、（0，5）．
同理，当顶点E在y轴右侧时，点F为（0，5）；
综上所述，S△EFG与S△ACD存在8倍的关系，点F坐标为（0，﹣60）、（0，3）、（0，5）．
【解析】（1）求出点A的坐标，利用顶点式求出抛物线的解析式；（2）①首先确定点E为Rt△BEF的直角顶点，相似关系为：△BAO∽△BFE；如答图2﹣1，作辅助线，利用相似关系得到关系式：BH=4FH，利用此关系式求出点E的坐标；②首先求出△ACD的面积：S△ACD=8；若S△EFG与S△ACD存在8倍的关系，则S△EFG=64或S△EFG=1；如答图2﹣2所示，求出S△EFG的表达式，进而求出点F的坐标．
【考点精析】掌握二次函数的性质是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
