题目内容
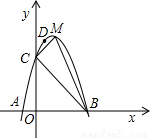
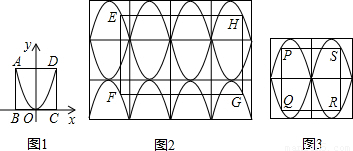
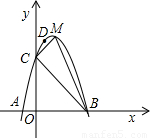
(2005•吉林)如图,过原点的直线l1:y=3x,l2:y= x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
(1)Sl关于t的函数解析式为______;(2)直线OC的函数解析式为______;
(3)S2关于t的函数解析式为______;(4)S3关于t的函数解析式为______.
【答案】分析:(1)把直线PQ的解析式分别与直线l1,l2的解析式联立,求出A,B两点坐标,用坐标表示三角形的底、高,运用割补法求S1;
(2)由于直线PQ与x轴的夹角为45°,根据正方形的性质可得,AC⊥x轴,BC∥x轴,C点横坐标与点A相同,纵坐标与点B相同,直线OC解析式可求;
(3)根据(1)(2)所得A、B、C三点坐标,可求AC,BC的长,从而,就可以表示S2了;
(4)用(2)的方法,可推出D点坐标( t,
t,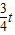 ),又P(t,0),可求直线PD解析式,从而可求点E的坐标,用S3=S△OEP-S△OAP可表示面积.
),又P(t,0),可求直线PD解析式,从而可求点E的坐标,用S3=S△OEP-S△OAP可表示面积.
解答:解:(1)∵直线l1与直线PQ相交于点A,
∴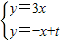 ,解得
,解得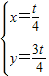 ,
,
∴A点坐标为( ,
,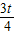 )
)
∵直线l2与直线PQ相交于点B,
∴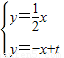 ,解得
,解得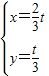
∴B点坐标为(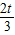 ,
,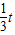 ).
).
∴S1=S△AOP-S△BOP=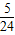 t2
t2
(2)由(1)得,点C的坐标为( ,
, ).
).
设直线OC的解析式为y=kx,根据题意得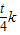 =
=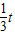 ,
,
∴k= ,
,
∴直线OC的解析式为y= x.
x.
(3)由(1)、(2)知,正方形ABCD的边长CB= t-
t-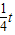 =
=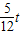 ,
,
∴S2=CB2=(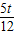 )2=
)2=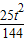 .
.
(4)设直线PD的解析式为y=k1x+b,由(1)知,点D的坐标为( t,
t,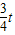 ),
),
将P(t,0)、D(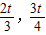 )代入得
)代入得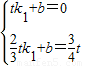 ,
,
解得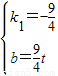
∴直线PD的解析式为y=- x+
x+ t.
t.
由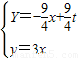 ,
,
得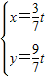
∴E点坐标为(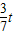 ,
, )
)
∴S3=S△EOP-S△AOP= t•
t• t-
t- t•
t• t=
t=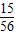 t2.
t2.
点评:本题考查了点的坐标求法,正方形的性质,采用了三角形面积的割补法表示面积.
(2)由于直线PQ与x轴的夹角为45°,根据正方形的性质可得,AC⊥x轴,BC∥x轴,C点横坐标与点A相同,纵坐标与点B相同,直线OC解析式可求;
(3)根据(1)(2)所得A、B、C三点坐标,可求AC,BC的长,从而,就可以表示S2了;
(4)用(2)的方法,可推出D点坐标(
 t,
t,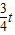 ),又P(t,0),可求直线PD解析式,从而可求点E的坐标,用S3=S△OEP-S△OAP可表示面积.
),又P(t,0),可求直线PD解析式,从而可求点E的坐标,用S3=S△OEP-S△OAP可表示面积.解答:解:(1)∵直线l1与直线PQ相交于点A,
∴
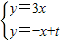 ,解得
,解得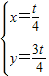 ,
,∴A点坐标为(
 ,
,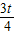 )
)∵直线l2与直线PQ相交于点B,
∴
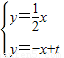 ,解得
,解得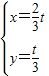
∴B点坐标为(
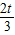 ,
,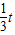 ).
).∴S1=S△AOP-S△BOP=
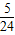 t2
t2(2)由(1)得,点C的坐标为(
 ,
, ).
).设直线OC的解析式为y=kx,根据题意得
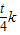 =
=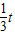 ,
,∴k=
 ,
,∴直线OC的解析式为y=
 x.
x.(3)由(1)、(2)知,正方形ABCD的边长CB=
 t-
t-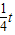 =
=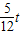 ,
,∴S2=CB2=(
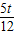 )2=
)2=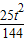 .
.(4)设直线PD的解析式为y=k1x+b,由(1)知,点D的坐标为(
 t,
t,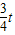 ),
),将P(t,0)、D(
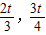 )代入得
)代入得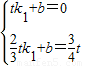 ,
,解得
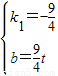
∴直线PD的解析式为y=-
 x+
x+ t.
t.由
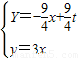 ,
,得
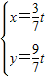
∴E点坐标为(
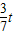 ,
, )
)∴S3=S△EOP-S△AOP=
 t•
t• t-
t- t•
t• t=
t=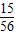 t2.
t2.点评:本题考查了点的坐标求法,正方形的性质,采用了三角形面积的割补法表示面积.

练习册系列答案
相关题目