题目内容
(2005•吉林)如图,已知一抛物线形大门,其地面宽度AB=18m.一同学站在门内,在离门脚B点1m远的D处,垂直地面立起一根1.7m长的木杆,其顶端恰好顶在抛物线形门上C处.根据这些条件,请你求出该大门的高h.
【答案】分析:解决抛物线的问题,需要合理地建立平面直角坐标系,用二次函数的性质解答,建立直角坐标系的方法有多种,大体是以抛物线对称轴为y轴(包括顶点在原点),抛物线经过原点等等.
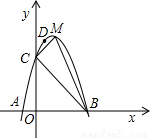
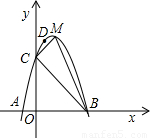
解答: 解:解法一:如图1,建立平面直角坐标系.
解:解法一:如图1,建立平面直角坐标系.
设抛物线解析式为y=ax2+bx.
由题意知B、C两点坐标分别为B(18,0),C(17,1.7),
把B、C两点坐标代入抛物线解析式得

解得
∴抛物线的解析式为
y=-0.1x2+1.8x
=-0.1(x2-18x+81-81)
=-0.1(x-9)2+8.1.
∴该大门的高h为8.1m.
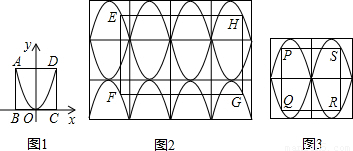
解法二:如图2,建立平面直角坐标系.
设抛物线解析式为y=ax2.
由题意得B、C两点坐标分别为B(9,-h),C(8,-h+1.7).
把B、C两点坐标代入y=ax2得

解得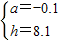
∴y=-0.1x2.
∴该大门的高h为8.1m.
说明:此题还可以以AB所在直线为x轴,AB中点为原点,建立直角坐标系,可得抛物线解析式为y=-0.1x2+8.1.
点评:建立适当的直角坐标系,根据题目所给数据求点的坐标,再求抛物线解析式,解答题目的问题.
解答:
 解:解法一:如图1,建立平面直角坐标系.
解:解法一:如图1,建立平面直角坐标系.设抛物线解析式为y=ax2+bx.
由题意知B、C两点坐标分别为B(18,0),C(17,1.7),
把B、C两点坐标代入抛物线解析式得

解得

∴抛物线的解析式为
y=-0.1x2+1.8x
=-0.1(x2-18x+81-81)
=-0.1(x-9)2+8.1.
∴该大门的高h为8.1m.
解法二:如图2,建立平面直角坐标系.

设抛物线解析式为y=ax2.
由题意得B、C两点坐标分别为B(9,-h),C(8,-h+1.7).
把B、C两点坐标代入y=ax2得

解得
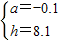
∴y=-0.1x2.
∴该大门的高h为8.1m.
说明:此题还可以以AB所在直线为x轴,AB中点为原点,建立直角坐标系,可得抛物线解析式为y=-0.1x2+8.1.
点评:建立适当的直角坐标系,根据题目所给数据求点的坐标,再求抛物线解析式,解答题目的问题.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目