Question

【题目】在平面直角坐标系中，抛物线经过点和．

（1）求抛物线的表达式和顶点坐标；

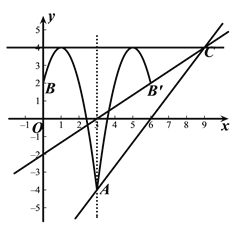
（2）将抛物线在A、B之间的部分记为图象M（含A、B两点）．将图象M沿直线翻折，得到图象N．若过点的直线与图象M、图象N都相交，且只有两个交点，求b的取值范围．

Answer 1

【答案】（1），（2）.

【解析】分析：（1）把A、B的坐标代入抛物线的解析式求出a、c的值，即可得到抛物线的解析式，从而得到抛物线的顶点坐标；

（2）先求出点关于的对称点为B’， 然后分别求出直线经过点和时b的值，直线经过点和时b的值，以及直线平行轴时b的值，即可得出结论．

详解：（1）∵抛物线经过点和，

可得：

解得：

∴抛物线的表达式为，∴，

∴顶点坐标为．

（2）设点关于的对称点为B’， 则点B’．

若直线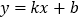经过点和，可得：．

若直线经过点和，可得．

直线平行轴时，．

综上所述：．