题目内容
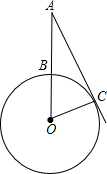如图，已知⊙O半径为8cm，点A为半径OB的延长线上一点，射线AC切⊙O于点C，弧BC的长为| 4 | 3 |
分析：首先根据弧长公式求出∠BOC的度数；在Rt△OCA中，可用未知数表示出AC、OA、AB的长，进而可由勾股定理列出方程，求出未知数的值，即可求得AB的长．
解答：解：∵弧BC的长为
πcm，
∴
π=
，
故∠BOC=30°，
设AC=x，则AO=2x；
（2x）2-x2=64
解得：x=
；
AB=AO-OB=2x-8=（
-8）cm．
| 4 |
| 3 |
∴
| 4 |
| 3 |
| n×π×8 |
| 180 |
故∠BOC=30°，
设AC=x，则AO=2x；
（2x）2-x2=64
解得：x=
8
| ||
| 3 |
AB=AO-OB=2x-8=（
16
| ||
| 3 |
点评：此题主要考查了切线的性质、弧长公式以及勾股定理的应用．
练习册系列答案
相关题目
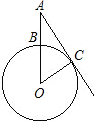如图，已知⊙O半径为8cm，点A为半径OB延长线上一点，射线AC切⊙O于点C，弧BC的长为
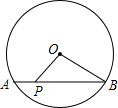如图，已知⊙O半径为5，弦AB长为8，点P为弦AB上一动点，连接OP，则线段OP的最小长度是
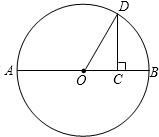如图，已知半径为R的半圆O，过直径AB上一点C，作CD⊥AB交半圆于点D，且CD=
单位的速度向下平移，设运动时间为t（t＞0），求t为何值时，直线MN再一次与⊙O1相切？（本小题保留3位有效数字）