Question

如图，已知半径为R的半圆O，过直径AB上一点C，作CD⊥AB交半圆于点D，且CD=

3

2

R，试求AC的长．

Answer 1

分析：由于点C的位置不能确定，故应分点C在A、O之间与C点在B、O之间两种情况画出图形，再根据勾股定理求解即可．

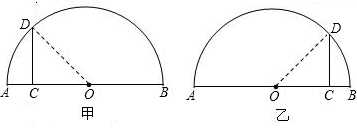
解答：解：（1）当C点在A、O之间时，如图甲．
由勾股定理OC=

R2-( 3 2 R)2

=

1

2

R，故AC=R-

1

2

R=

1

2

R；
（2）当C点在B、O之间时，如图乙．
由勾股定理知OC=

R2-( 3 2 R)2

=

1

2

R，故AC=R+

1

2

R=

3

2

R．
故答案为：

1

2

R或

3

2

R．

点评：本题考查的是圆心角、弧、弦的关系及勾股定理，解答此题的关键是分两种情况画出图形，再利用勾股定理求解．