题目内容
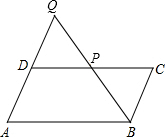 (2011•梅州)如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.
(2011•梅州)如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
分析:(1)由图可知∠QPD=∠CPB(对顶角),又AD平行于BC,所以∠QDP=∠CPB,所以△DQP与△CBP相似;
(2)△DQP≌△CBP,DP=CP=
CD,AB=CD=8,继而即可得出答案.
(2)△DQP≌△CBP,DP=CP=
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AQ∥BC,
∴∠QDP=∠BCP,
又∠QPD=∠CPB,
∴△DQP∽△CBP;
(2)解:∵△DQP≌△CBP,
∴DP=CP=
CD,
∵AB=CD=8,
∴DP=4.
∴AQ∥BC,
∴∠QDP=∠BCP,
又∠QPD=∠CPB,
∴△DQP∽△CBP;
(2)解:∵△DQP≌△CBP,
∴DP=CP=
| 1 |
| 2 |
∵AB=CD=8,
∴DP=4.
点评:本题考查平行四边形、全等三角形的性质及相似三角形的判定,解题关键是对这些知识的熟练掌握,难度一般.

练习册系列答案
相关题目
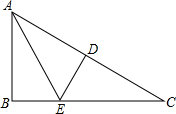 (2011•梅州)如图,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为
(2011•梅州)如图,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为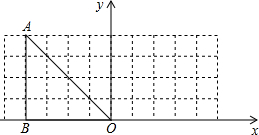 绕原点O按顺时针方向旋转135°得到△A1B1O.回答下列问题:(直接写结果)
绕原点O按顺时针方向旋转135°得到△A1B1O.回答下列问题:(直接写结果)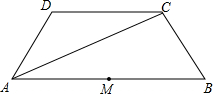 边AB的中点M重合.
边AB的中点M重合.