Question

【题目】下列结论错误的是（ ）

A.全等三角形对应边上的中线相等

B.两个直角三角形中，两个锐角相等，则这两个三角形全等

C.全等三角形对应边上的高相等

D.两个直角三角形中，斜边和一个锐角对应相等，则这两个三角形全等

Answer 1

【答案】B

【解析】

试题分析：画出图形，根据全等三角形的性质和判定（全等三角形的判定定理有SAS，ASA，AAS，SSS）判断即可.

解：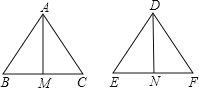

A、∵△ABC≌△DEF，

∴AB=DE，∠B=∠E，BC=EF，

∵AM是△ABC的中线，DN是△DEF中线，

∴BC=2BM，EF=2EN，

∴BM=EN，

在△ABM和△DEN中

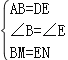
∴△ABM≌△DEN（SAS），

∴AM=DN，正确，故本选项错误；

B、如教师用得含30度的三角板和学生用的含30度的三角板就不全等，错误，故本选项正确；

C、

∵△ABC≌△DEF，

∴AB=DE，∠B=∠E，

∵AM是△ABC的高，DN是△DEF的高，

∴∠AMB=∠DNE=90°，

在△ABM和△DEN中

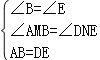
∴△ABM≌△DEN，

∴AM=DN，正确，故本选项错误；

D、根据AAS即可推出两直角三角形全等，正确，故本选项错误；

故选B.