题目内容
已知,如图①,在平行四边形ABCD中,AB=12,BC=6,AD⊥BD。以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=300,∠AED=900。
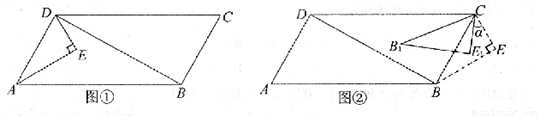
(1)求△AED的周长;
(2)若△AED以每秒2个长度单位的速度沿DC向右平行移动,得到△A0E0D0,当A0D0与BC重合时停止移动。设移动时间为t秒,△A0E0D0与△BDC重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出t的取值范围;
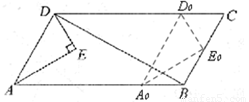
(3)如图②,在(2)中,当△AED停止移动后得到△BEC,将△BEC绕点C按顺时针方向旋转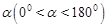 ,在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q。是否存在这样的
,在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q。是否存在这样的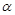 ,使△BPQ为等腰三角形?若存在,求出
,使△BPQ为等腰三角形?若存在,求出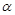 的度数;若不存在,请说明理由。
的度数;若不存在,请说明理由。
解:(1)在平行四边形ABCD中, BC=6,∴AD= BC=6。
∵在Rt△AED中,∠EAD=300,∠AED=900,∴DE=3,AE=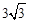 。
。
∴△AED的周长为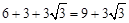 。
。
(2)S与t之间的函数关系式为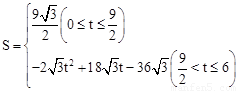 。
。
(3)存在。分三种情况讨论:
①若BP=BQ,如图,则
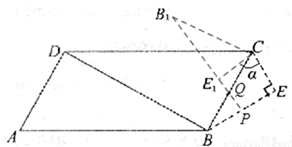
∵∠PBQ=300,
∴∠BQP=∠BPQ=750。
∴∠E1QC=∠BQP=750。
∴∠E1CQ=900-750=150。
∴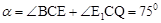 。
。
②若PQ=BQ,如图,则

∵∠PBQ=300,
∴∠BQP=1200。
∴∠B1QC=∠BQP=1200。
∴∠B1CQ=1800-1200-300=300。
∴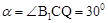 。
。
③若PQ=BP,如图,则
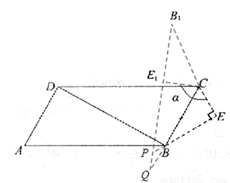
∵∠CBE =300,
∴∠PBQ=300。
∴∠BQP=∠PBQ=300。
∴∠E1CQ=900-300=600。
∴ 。
。
根据等腰三角形三线合一的性质,此时B、P、Q三点重合。
∴此时不存在这样的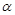 ,使△BPQ为等腰三角形。
,使△BPQ为等腰三角形。
综上所述,存在这样的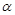 ,使△BPQ为等腰三角形,
,使△BPQ为等腰三角形,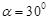 或
或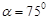 。
。
【解析】(1)根据平行四边形对边相等可得AD= BC=6,在Rt△AED中根据含30度角直角三角形的性质可得DE=3,AE=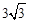 ,从而可求△AED的周长。
,从而可求△AED的周长。
(2)如图,当△AED移动到点E0在BC边上时,易得△CD0E0是等边三角形,故在D0C=3,△AED移动的距离DD0=12-3=9,从而由速度为每秒2个长度单位,得△AED移动的时间为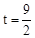 。
。
当A0D0与BC重合时,△AED移动的距离为DC=12,由速度为每秒2个长度单位,得△AED移动的时间为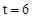 。
。
∴当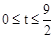 时,
时,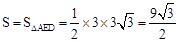 。
。
当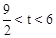 时,如图,
时,如图,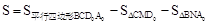 ,
,
过点D0作在D0H⊥BC于点H,过点N作NG⊥AB于点G,则
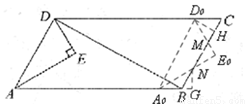
DD0=2t,D0C=A0B=BN=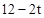 ,∴
,∴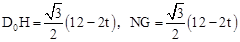 。
。
∴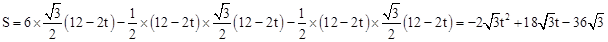 。
。
当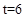 时,
时,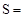 0,满足上式。
0,满足上式。
综上所述,S与t之间的函数关系式为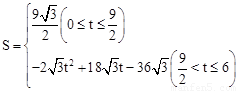 。
。
(3)分BP=BQ,PQ=BQ,PQ=BP三种情况讨论即可。


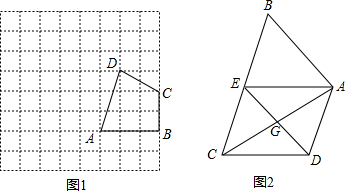

 相交于点C.
相交于点C.
