题目内容
【题目】如图1,抛物线![]() 与x轴相交于A、B两点(点A在点B的右侧),已知C(0,
与x轴相交于A、B两点(点A在点B的右侧),已知C(0,![]() ).连接AC.
).连接AC.
(1)求直线AC的解析式.
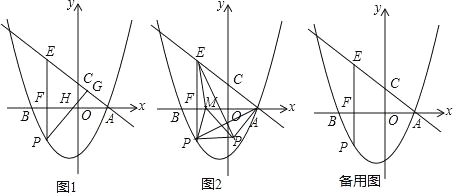
(2)点P是x轴下方的抛物线上一动点,过点P作PE⊥x轴交直线AC于点E,交x轴于点F,过点P作PG⊥AE于点G,线段PG交x轴于点H.设l=EP﹣![]() FH,求l的最大值.
FH,求l的最大值.
(3)如图2,在(2)的条件下,点M是x轴上一动点,连接EM、PM,将△EPM沿直线EM折叠为△EP1M,连接AP,AP1.当△APP1是等腰三角形时,试求出点M的坐标.
【答案】(1)y=﹣![]() (2)当m=﹣2时,l最大=4(3)M1(3
(2)当m=﹣2时,l最大=4(3)M1(3![]() ﹣8,0),M2(2,0),M3(﹣3
﹣8,0),M2(2,0),M3(﹣3![]() ﹣8,0),M4(﹣
﹣8,0),M4(﹣![]() ,0)
,0)
【解析】
试题分析:(1)先令y=0求抛物线与x轴交点坐标,利用待定系数法求直线AC的解析式;
(2)如图1中,设点P(m,![]() m2+
m2+![]() m﹣3),则E(m,﹣
m﹣3),则E(m,﹣![]() m+
m+![]() ),构建关于x的二次函数,利用二次函数的性质即可解决问题.
),构建关于x的二次函数,利用二次函数的性质即可解决问题.
(3)如图2中,分四种情形讨论即可①当P1P=P1A时,②AP=AP2时,③当P3P=P3A时,④当P4P=PA时,画出图形,求出点M坐标即可.
试题解析:(1)当y=0时,![]() x2+
x2+![]() x﹣3=0,解得x1=﹣3,x2=2,
x﹣3=0,解得x1=﹣3,x2=2,
∵点A在点B的右侧,
∴A(2,0)、B(﹣3,0);
设直线AC的解析式为y=kx+b,
把A(2,0)、C(0,![]() )代入得:
)代入得: 解得
解得 ,
,
∴直线AC的解析式为:y=﹣![]() ;
;
(2)如图1中,在Rt△ACO中,tan∠OAC=![]() =
=![]()
∵∠FPH+∠PHF=90°,∠OAC+∠AHG=90°,∠PHF=∠AHG,
∴∠HPF=∠OAC
∴tan∠FPH=tan∠OAC=![]()
∵tan∠FPH=![]()
∴![]() FH=
FH=![]() ×FP×
×FP×![]() =
=![]() FP
FP
设点P(m,![]() m2+
m2+![]() m﹣3),则E(m,﹣
m﹣3),则E(m,﹣![]() m+
m+![]() ),
),
∴EP=﹣![]() m2﹣
m2﹣![]() m+
m+![]() ,FP=﹣
,FP=﹣![]() m2﹣
m2﹣![]() m+3,
m+3,
于是l=EP﹣![]() FH=EP﹣
FH=EP﹣![]() FP=﹣
FP=﹣![]() m2﹣m+3,
m2﹣m+3,
∵﹣![]() <0
<0
∴l=﹣![]() m2﹣m+3开口向下,对称轴x=
m2﹣m+3开口向下,对称轴x=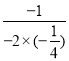 =﹣2,
=﹣2,
∵点P是x轴下方的抛物线上一动点,
∴﹣3<m<2
∴在﹣3<m<2时,当m=﹣2时,l最大=4;
(3)如图2中,m=﹣2时,E(﹣2,3),P(﹣2,﹣2),
∵A(2,0),
∴EP=EA=5,
①当P1P=P1A时,AP中点K(0,﹣1),于是直线EK为y=﹣2x﹣1,
∴直线EK交x于I(﹣![]() ,0),EI=
,0),EI=![]() ,
,
过点M1作M1J⊥EK于J,则EJ=EF=3,
∴IJ=![]() ﹣3,
﹣3,
∵△IEF∽△IM1J,
∴![]() ,
,
∴IM1=![]() ﹣3
﹣3![]() .
.
∴M1(3![]() ﹣8,0),
﹣8,0),
②AP=AP2时,△AEP≌△AEP2,
∴∠AEP=∠AEP2,
∴点M2与点A重合,
∴点M2(2,0).
③当P3P=P3A时,由△EFM3∽△M1FE,得到EF2=FM3FM1,
∴FM3=3![]() +6,
+6,
∴点M3(﹣3![]() ﹣8,0),
﹣8,0),
④当P4P=PA时,作M4Q⊥EP4,设M4Q=M4F=x,
在RT△P4QM4中,
∵P4Q2+QM42=FP42,
∴22+x2=(4﹣x)2,
∴x=![]() ,
,
∴0M4=![]() +2=
+2=![]() ,
,
∴点M4(﹣![]() ,0).
,0).
综上所述点M1(3![]() ﹣8,0),M2(2,0),M3(﹣3
﹣8,0),M2(2,0),M3(﹣3![]() ﹣8,0),M4(﹣
﹣8,0),M4(﹣![]() ,0).
,0).



【题目】为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如表:
每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
人数 | 2 | 5 | 8 | 9 | 6 |
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.4,3
B.4,3.5
C.3.5,3.5
D.3.5,4
【题目】某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
求A、B两种型号的电风扇的销售单价.