题目内容
(2005•山西)某中学库存960套旧桌凳,修理后捐助贫困山区学校现有甲、乙两个木工小组都想承揽这项业务.经协商后得知:甲小组单独修理这批桌凳比乙小组多用20天;乙小组每天比甲小组多修8套;学校每天需付甲小组修理费80元,付乙小组120元.(1)求甲、乙两个木工小组每天各修桌凳多少套?
(2)在修理桌凳过程中,学校要委派一名维修工进行质量监督,并由学校负担他每天10元的生活补助.现有以下三种修理方案供选择:①由甲单独修理;②由乙单独修理;③由甲、乙共同合作修理.你认为哪种方案既省时又省钱?试比较说明.
【答案】分析:(1)关键描述语为:“甲小组单独修理这批桌凳比乙小组多用20天”;等量关系为:甲小组单独修理这批桌凳的时间=乙小组单独修理这批桌凳的时间+20.
(2)必须每种情况都考虑到,求出每种情况下实际花费,进行比较.
解答:解:(1)设甲小组每天修桌凳x套.
则: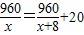 .
.
整理得:x2+8x-384=0.
解得:x1=-24(舍去),x2=16.
经检验:x=16是原方程的解.
∴x+8=24.
答:甲小组每天修桌凳16套,乙小组每天修24套.
(2)若甲小组单独修理,则需960÷16=60(天);
总费用:60×80+60×10=5400(元).
若乙小组单独修理,则需960÷24=40(天);
总费用:40×120+40×10=5200(元).
若甲、乙两小组合作:则需960÷(24+16)=24(天)
总费用:(80+120)×24+24×10=5040(元)
通过比较看出:选择第三种方案符合既省时,又省钱的要求.
点评:列分式方程解应用题与所有列方程解应用题一样,重点在于准确地找出相等关系,这是列方程的依据.
(2)必须每种情况都考虑到,求出每种情况下实际花费,进行比较.
解答:解:(1)设甲小组每天修桌凳x套.
则:
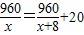 .
.整理得:x2+8x-384=0.
解得:x1=-24(舍去),x2=16.
经检验:x=16是原方程的解.
∴x+8=24.
答:甲小组每天修桌凳16套,乙小组每天修24套.
(2)若甲小组单独修理,则需960÷16=60(天);
总费用:60×80+60×10=5400(元).
若乙小组单独修理,则需960÷24=40(天);
总费用:40×120+40×10=5200(元).
若甲、乙两小组合作:则需960÷(24+16)=24(天)
总费用:(80+120)×24+24×10=5040(元)
通过比较看出:选择第三种方案符合既省时,又省钱的要求.
点评:列分式方程解应用题与所有列方程解应用题一样,重点在于准确地找出相等关系,这是列方程的依据.

练习册系列答案
相关题目
(2005•山西)某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
| 加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(2)假如生产部负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
 -1米,则需安装闪光灯( )
-1米,则需安装闪光灯( )