题目内容
 如图所示的半圆中,AD是直径,且AD=3,AC=2,则cos∠B的值是
如图所示的半圆中,AD是直径,且AD=3,AC=2,则cos∠B的值是
- A.

- B.

- C.

- D.

C
分析:根据AD是直径,∠B=∠D,且AD=3,AC=2,CD= ,根据在直角△ACD中,利用余弦值等于这个角的邻边比斜边,即可得出答案.
,根据在直角△ACD中,利用余弦值等于这个角的邻边比斜边,即可得出答案.
解答:∵如图所示的半圆中,AD是直径,且AD=3,AC=2,
∴∠ACD=90°,∠B=∠D,CD= ,
,
∴cos∠B=cos∠D= =
= .
.
故选C.
点评:此题主要考查了圆周角的性质以及勾股定理和锐角三角函数的定义,正确的转化cos∠B=cos∠D是解决问题的关键.
分析:根据AD是直径,∠B=∠D,且AD=3,AC=2,CD=
 ,根据在直角△ACD中,利用余弦值等于这个角的邻边比斜边,即可得出答案.
,根据在直角△ACD中,利用余弦值等于这个角的邻边比斜边,即可得出答案.解答:∵如图所示的半圆中,AD是直径,且AD=3,AC=2,
∴∠ACD=90°,∠B=∠D,CD=
 ,
,∴cos∠B=cos∠D=
 =
= .
.故选C.
点评:此题主要考查了圆周角的性质以及勾股定理和锐角三角函数的定义,正确的转化cos∠B=cos∠D是解决问题的关键.

练习册系列答案
相关题目
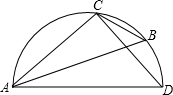 如图所示的半圆中,AD是直径,且AD=3,AC=2,则cos∠B的值是( )
如图所示的半圆中,AD是直径,且AD=3,AC=2,则cos∠B的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
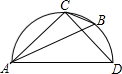 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是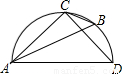 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .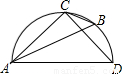 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .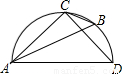 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .