题目内容
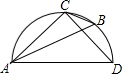如图所示的半圆中，AD是直径，且AD=3，AC=2，则sinB的值是分析：根据圆周角定理得到∠ADC=∠B，因而sinB=sin∠ADC=
．
| AC |
| AD |
解答：解：∵AD是直径，
∴∠ACD=90°．
∵AD=3，AC=2，
∴sinADC=
=
．
∵∠ADC=∠B，
∴sinB=
．
∴∠ACD=90°．
∵AD=3，AC=2，
∴sinADC=
| AC |
| AD |
| 2 |
| 3 |
∵∠ADC=∠B，
∴sinB=
| 2 |
| 3 |
点评：本题考查了圆中圆周角的转化和直角三角形三角函数的求解，决定三角函数值大小的是角的大小，只要角的大小相同，函数值就相同．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
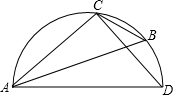如图所示的半圆中，AD是直径，且AD=3，AC=2，则cos∠B的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示的半圆中，AD是直径，且AD=3，AC=2，则sinB的值是 ．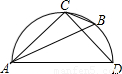
如图所示的半圆中，AD是直径，且AD=3，AC=2，则sinB的值是 ．
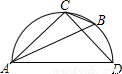如图所示的半圆中，AD是直径，且AD=3，AC=2，则sinB的值是 ．