Question

如图，在四边形纸片ABCD中，已知：AD∥BC，AB∥CD，∠B=90°，现将四边形纸片ABCD对折，折痕为PF（点P在BC上，点F在DC上），使顶点C落在四边形ABCD内一点C′，PC′的延长线交AD于M，再将纸片的另一部分对折（折痕为ME），使顶点A落在直线PM上一点A′.

（1）填空：
因为AD∥BC，（已知）
所以∠B+∠A=180°（            ）
又因为∠B=90°（已知）
所以∠A=      度.
则：∠EA′M=    度.
又因为AB∥CD（已知）
同理：∠FC′P=∠C=     度.
所以∠EA′M     ∠FC′P（填 “＜”或“=”或“＞”）
所以       ∥     理由：（              ）.
（2）ME与PF平行吗？请说明理由.

Answer 1

解：（1）两直线平行，同旁内角互补，90，90，90，=，EA′，FC′,内错角相等，两直线平行.……………………4分
（2）答：EM∥PF……………5分
理由：因为AD∥BC（已知）
所以∠AMP=∠CPM（两直线平行，内错角相等）
由对折可知：∠EMP=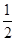∠AMP，∠F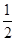PM=∠CPM
所以∠EMP=∠FPM
EM∥PF（内错角相等，两直线平行）
…………………………………………10分

解析