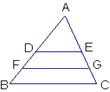
题目内容
 如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则
如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则(1)
| DF |
| BC |
| 1 |
| 4 |
| 1 |
| 4 |
(2)
| S△AGC |
| S△BGC |
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)因为DE是△ABC的中位线,所以DE=
BC,因为F是DE的中点,所以DF是BC的
,问题得解;
(2)因为△AGC和△BGC中BG和AG边上的高相等,所以其面积比可转化为底之比即AG:BG的比值,过E作EM∥AB与GC交于点M,构造全等三角形把DG转移到和AG有关的中位线处,可得所求线段的比,进而求出面积比.
| 1 |
| 2 |
| 1 |
| 4 |
(2)因为△AGC和△BGC中BG和AG边上的高相等,所以其面积比可转化为底之比即AG:BG的比值,过E作EM∥AB与GC交于点M,构造全等三角形把DG转移到和AG有关的中位线处,可得所求线段的比,进而求出面积比.
解答:解:(1)∵DE是△ABC的中位线,
∴DE=
BC,
∵F是DE的中点,
∴DF=
DE,
∴DF=
BC,
∴
=
;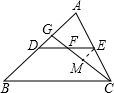
(2)过E作EM∥AB与GC交于点M,
∴△EMF≌△DGF,
∴EM=GD,
∵DE是中位线,
∴CE=
AC,
又∵EM∥AG,
∴△CME∽△CGA,
∴EM:AG=CE:AC=1:2,
又∵EM=GD,
∴AG:GD=2:1,
∵D是AB中点,
∴AD=BD,
∴BG:AG=2:1,
∴
=
,
故答案为:
;
.
∴DE=
| 1 |
| 2 |
∵F是DE的中点,
∴DF=
| 1 |
| 2 |
∴DF=
| 1 |
| 4 |
∴
| DF |
| BC |
| 1 |
| 4 |

(2)过E作EM∥AB与GC交于点M,
∴△EMF≌△DGF,
∴EM=GD,
∵DE是中位线,
∴CE=
| 1 |
| 2 |
又∵EM∥AG,
∴△CME∽△CGA,
∴EM:AG=CE:AC=1:2,
又∵EM=GD,
∴AG:GD=2:1,
∵D是AB中点,
∴AD=BD,
∴BG:AG=2:1,
∴
| S△AGC |
| S△BGC |
| 1 |
| 2 |
故答案为:
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查三角形中位线定理和全等三角形的性质,由中点构造全等三角形,从而将求解同一直线上的两条线段的比值问题转化为不共线的两条线段的比值问题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
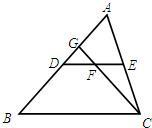 如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )| A、2:1 | B、3:1 | C、3:2 | D、4:3 |
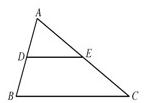 10、如图DE是△ABC的中位线,已知BC=6cm,那么DE长是
10、如图DE是△ABC的中位线,已知BC=6cm,那么DE长是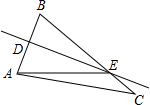 已知,如图DE是△ABC的边AB的垂直平分线,D为垂足,DE交BC于E,且AC=5,BC=8,则△AEC的周长为
已知,如图DE是△ABC的边AB的垂直平分线,D为垂足,DE交BC于E,且AC=5,BC=8,则△AEC的周长为