题目内容
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CPQ与△CBA相似,所需要的时间是多少秒?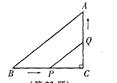

 或
或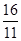
设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①Rt△ABC∽Rt△QPC则AC/ BC =" QC/" PC ,即3/ 4 =" t/" (4-2t) 解之得t= ;
;
②若Rt△ABC∽Rt△PQC则PC /QC =" AC/BC" ,(4-2t)/ t =" 3" /4 解之得t=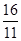 ;
;
由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<2,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为 或
或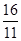 秒
秒
若两三角形相似,则由相似三角形性质可知,其对应边成比例,据此可解出两三角形相似时所需时间.
①Rt△ABC∽Rt△QPC则AC/ BC =" QC/" PC ,即3/ 4 =" t/" (4-2t) 解之得t=
 ;
;②若Rt△ABC∽Rt△PQC则PC /QC =" AC/BC" ,(4-2t)/ t =" 3" /4 解之得t=
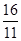 ;
;由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<2,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为
 或
或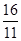 秒
秒若两三角形相似,则由相似三角形性质可知,其对应边成比例,据此可解出两三角形相似时所需时间.

练习册系列答案
相关题目
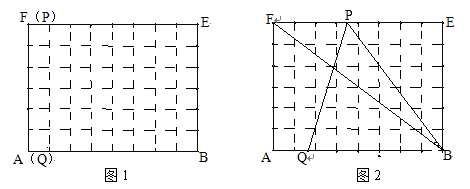
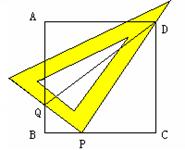
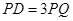 ,请证明你的结论;
,请证明你的结论;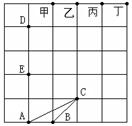
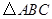 顶点
顶点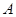 的坐标为
的坐标为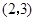 ,若以原点O为位似中心,画
,若以原点O为位似中心,画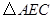 的位似图形
的位似图形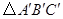 ,使
,使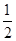 ,则点
,则点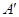 的坐标为 .
的坐标为 .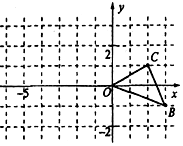
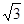
 .
. .
.